問題演習コーナー
【問題】10%の食塩水Aが100gあります。Aに5%の食塩水Bを5g加えてよくかき混ぜ、1回の操作とします。このとき、次の問いに答えましょう。
(1) 5回目の操作が終わった後、Aの濃度は何%になっていますか。
(2) Aの濃度が初めて8%以下になるのは、何回目の操作が終わった後ですか。
(1)の解答(食塩水の濃度を求める)
10%の食塩水A100gと5%の食塩水B25g(=5g×5回)を混ぜ合わせると考えます。それぞれの食塩水に溶けている食塩の重さを求めます。
A100gに溶けている食塩の重さは100×0.1=10(g)です。B25gに溶けている食塩の重さは25×0.05=1.25(g)です。
したがって、「食塩の重さ÷食塩水の重さ=濃度(小数)」より、(10+1.25)÷(100+25)=0.09です。これを100倍して9%が答です。
別解1(面積図を利用した解き方)
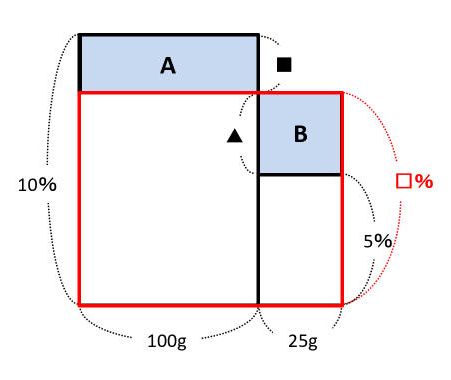
上の図の□を求めます。
長方形Aの面積と長方形Bの面積は等しいので、長方形Aの高さを■、長方形Bの高さを▲とすると、■×100=▲×25です。この式を逆比の関係に書きかえて、■:▲=25:100=1:4です。また、■+▲=10-5=5なので、■=5÷(1+4)×1=1と求められます。したがって、□=10-■=10-1=9(%)が答です。
別解2(天秤図を利用した解き方)
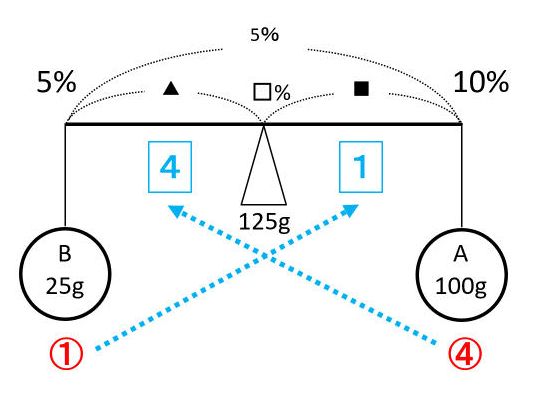
上の図の□を求めます。
食塩水の重さの比がA:B=100:25=4:1なので、濃度の比がA:B=■:▲=1:4です。天秤の腕全体の長さは10-5=5(%)なので、■=5÷(1+4)×1=1(%)となり、□=10-1=9(%)が答です。
(2)の解答(操作回数を求める問題)
面積図や天秤図で解きにくい問題は、□を使った式を作って解きます。
□回目の操作が終わった後、Aの濃度が8%になったとします。このとき、10%の食塩水A100gと5%の食塩水B(5×□)g(=5g×□回)を混ぜ合わせたことになります。
B 5gに溶けている食塩の重さは5×0.05=0.25(g)なので、B(5×□)gに溶けている食塩の重さは(0.25×□)gです。
したがって、「食塩の重さ÷食塩水の重さ=濃度(小数)」より、(10+0.25×□)÷(100+5×□)=0.08です。これを解いて□を求めます。
(10+0.25×□)÷(100+5×□)=0.08
10+0.25×□=0.08×(100+5×□)
10+0.25×□=8+0.40×□
(0.40-0.25)×□=10-8
0.15×□=2
□=2÷0.15=13.33…
回数は整数でなければならないので、14回目が答です。(13回目だと8%以下にならないので注意しましょう)
① 食塩水の濃度(濃さ)とは何ですか。
(例)食塩水の中に溶けている食塩の重さの割合です。
② 食塩水の重さ・食塩の重さ・濃度は、それぞれ割合の式の何に当たりますか。
(例)食塩水の重さはもとにする量、食塩の重さはくらべる量(くらべられる量)、濃度は割合に当たります。
③ 濃度の変化を考える問題では、何に着目しますか。
(例)食塩の重さに着目します。
④ 天秤図では、食塩水の重さと濃度を何で表しますか。
(例)食塩水の重さをおもりで、食塩水の濃度をおもりから支点までの腕の長さで表します。
トップ画像=写真AC



コメント
参考になりました。
ありがとうございました。
お役に立てたようで何よりです。
頑張ってください。
わかりやすい解説ありがとうございます•̀ᴗ-
おかげで塾の宿題が完璧に終わりました!
お役に立ててうれしいです!
食塩水の濃度は解き方がいろいろありますので、
自分に合った解き方を見つけてもらえればと思います。