数学の平面図形分野では、円に内接する図形の角度を求める問題が頻出です。このとき、「同じ弧に対する円周角の大きさは等しい」という円周角の定理を使います。この定理を利用して大きさの等しい円周角を見つける手順について解説します。
大きさの等しい円周角を見つける手順
次の図で、∠DAEと大きさの等しい円周角を全て見つけてみてください。
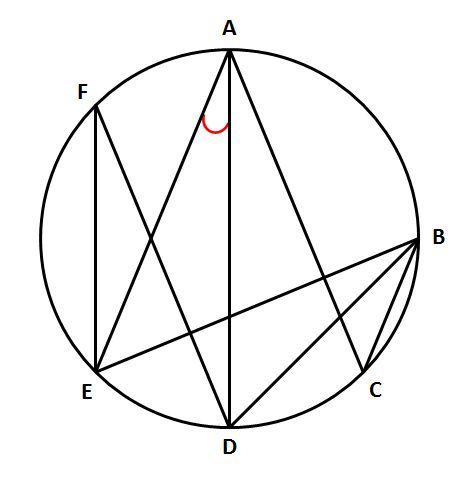
これにパッと答えられない場合は、次の手順で考えるといいでしょう。
- 円周角を作る直線をなぞる。
- 1で円周角に対する弧を見つける。
- 2の弧から伸びる直線をなぞる。
手順通りに、∠DAEと大きさの等しい円周角を探します。
∠DAEを作る直線を指でなぞっていくと、それらが円周とぶつかる点Dと点Eを見つけられるはずです。これら2点が作る弧DEが∠DAEに対する弧です。
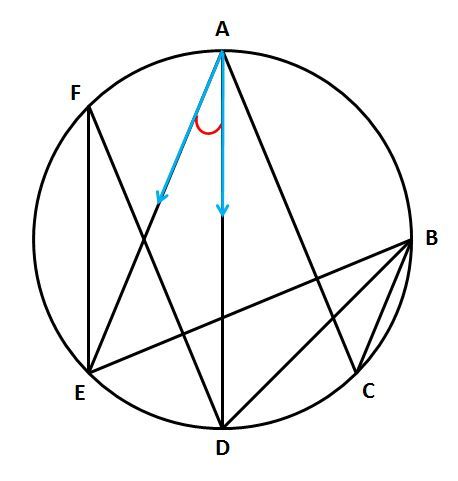
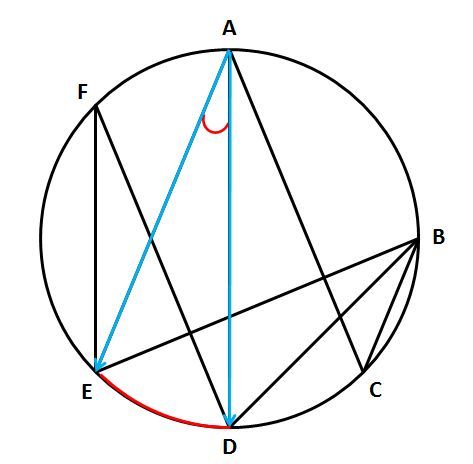
今度は逆に、点Dと点Eから伸びる直線をなぞってみましょう。
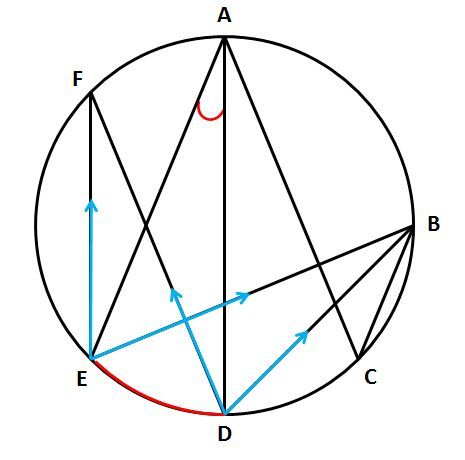
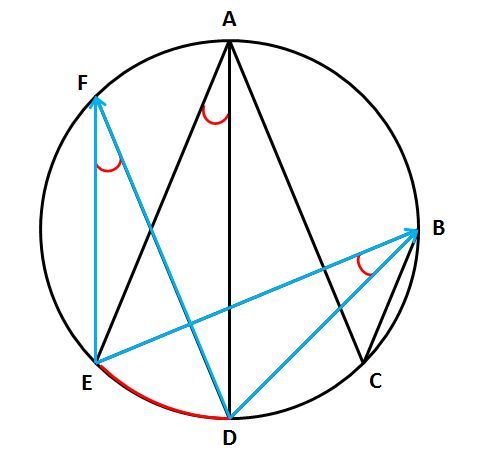
ADとAEを除いたBD、BE、FD、FEの4本をズーッとたどっていきます。これら4本が円周とぶつかるところに円周角ができます。そして、円周角である∠DBEと∠DFEが弧DEに対する円周角で、∠DAEと大きさの等しいとわかります。
大きさの等しい円周角を見つける手順はとても簡単です。
円周角の問題を解いてみよう
大きさの等しい円周角を見つける手順を使って、次の図形の∠AEDの大きさを求めましょう。ただし、点Oは円の中心とします。
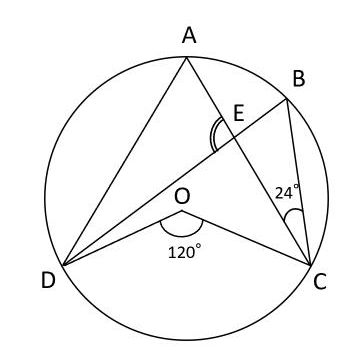
∠AEDは円周角ではありません。そのため、△AEDに着目して、三角形の内角の和が180°であることから∠AEDを求めます。このとき大きさが必要となる角度は∠ADEと∠DAEです。そして、これら2つの角は円周角です。大きさのわからない円周角があるときは、同じ弧に対する円周角を探しましょう。
まずは、∠ADEについて考えます。∠ADEを作る直線を指でなぞっていって、∠ADEに対する弧ABを見つけます。そして、点Aと点Bから伸びる直線を指でなぞって、弧ABに対する円周角∠ACBを見つけます。これより、∠ADE=∠ACB=24°です。
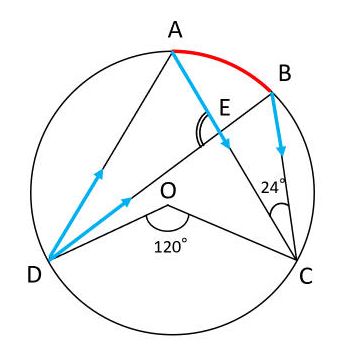
次に、∠DAEについて考えます。∠DAEを作る直線を指でなぞっていって、∠DAEに対する弧CDを見つけます。そして、点Cと点Dから伸びる直線を指でなぞっていきます。弧CDに対する円周角∠CBDの大きさは不明なので、円周角ではなく中心角∠CODに着目します。同じ弧に対する円周角は中心角の半分なので、∠DAE=∠COD÷2=60°です。
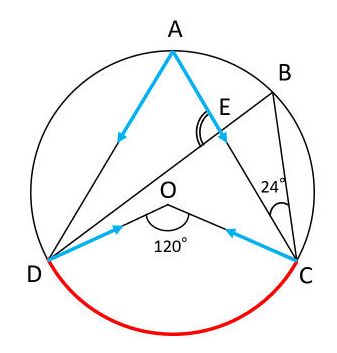
したがって、三角形の内角の和から、∠AED=180°-(∠ADE+∠DAE)=180°-(24°+60°)=96°が答です。
円周角を見つけるのは楽しい!
円に内接する図形の角度を求める問題の中には複雑な問題もあります。そういう問題でも、「大きさの等しい円周角を見つけてみよう!」という気持ちで図形を眺めていると、「あっ!」と気づく瞬間があります。中高生の皆さんは、この気付きを楽しんでみてください。
トップ画像=Pixabay



コメント