比の応用問題に「倍数算」があります。倍数算とは、2つの数が増えたり減ったりするとき、変化の前や後の数を求める特殊算です。
計算だけで解こうとするとこんがらがる倍数算を線分図で解いてみましょう。
差が一定の倍数算を解いてみよう
算数の問題集などには、次のような解き方が書かれています。
2人の所持金の差の比は、本を買う前が4－3＝1、本を買った後が5－3＝2です。
2人の所持金の差は一定なので（変わらないので）、差の比の1と2を最小公倍数の2にそろえます。本を買う前が8－6＝2、本を買った後が5－3＝2となりました。
A君の所持金に注目して、本を買う前と本を買った後の所持金の差の比は8－5＝3です。したがって、比の1にあたる金額は900÷3＝300円とわかります。
A君のもとの所持金の比は8なので、300×8＝2400円が答です。
何をしているのか、よくわからないなぁ……
それなら、線分図を描いてみると、わかりやすいよ。
同じ長さの線分に注目しよう
2人の所持金を2本の線分図で表してみます。
ポイントは、4：3と5：3を区別するために○と□を使うことと、2人とも同じ本を買ったので900円を左に寄せて描くことです。
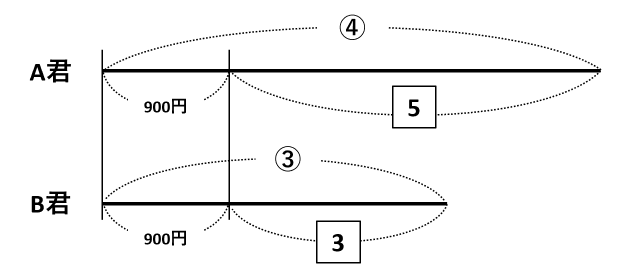
下の図に書き足した赤い線分が2人の所持金の差です。
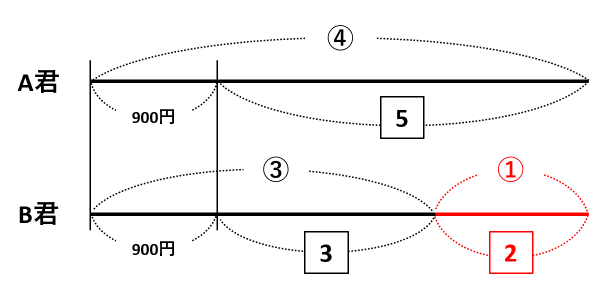
①と2は同じ長さなので、①と2の最小公倍数の2にそろえます。そうすると、下の図のように、④→8、③→6になります。
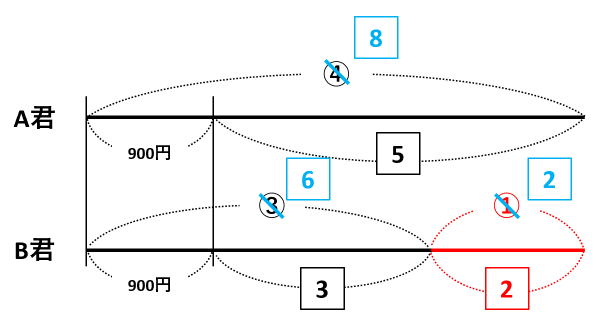
8－5＝3＝900円なので、1＝900÷3＝300円です。A君のもとの所持金は8なので、300×8＝2400円が答です。
「差が一定（変わらない）」というのは、線分図の右を見ればいいのね！
比を最小公倍数にそろえよう
線分図の描き方によっては、差が一定であることに気づきにくくなります。たとえば、次の線分図のように、900円を右に書いた場合です。
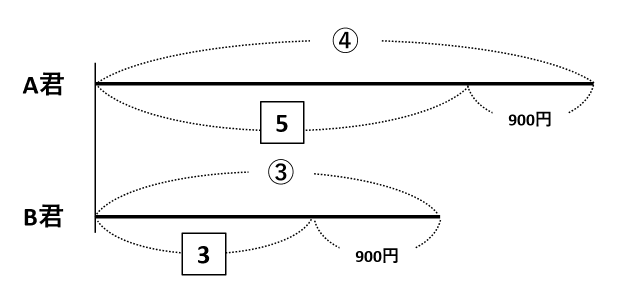
このような線分図で考えるなら、○か□のどちらかの比を最小公倍数にそろえてしまいましょう。
下の図では、④と③を最小公倍数の⑫にそろえました。
上の線分は、④を4倍したので、5と900円も5倍しました。一方、下の線分は、③を3倍したので、3と900円も3倍しました。
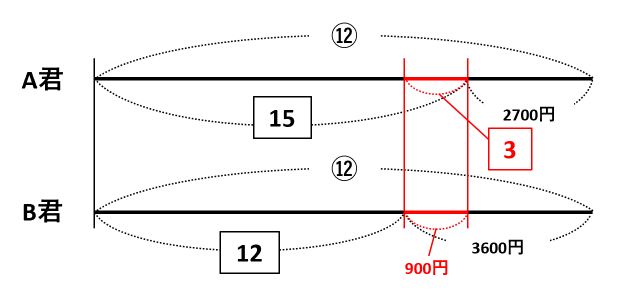
赤い線分に注目して、15－12＝3、3600－2700＝900円なので、3＝900円です。したがって、1＝900÷3＝300円とわかりました。
A君のもとの所持金は5＋900なので、300×5＋900＝2400円が答です。
5と3を15にそろえても解けるよ。興味のある受験生はチャレンジしてみよう！
○か□のどちらかの比を最小公倍数にそろえる解き方は、差が一定でなくても使えます。どんな倍数算でも解けるようになりたければ、こちらの解き方に慣れておくとよいでしょう。
和が一定の倍数算を解いてみよう
【例題2】は、最初から線分図で解説します。
2人でお金をやりとりする倍数算のポイントは、1本の線分図で表すことです。
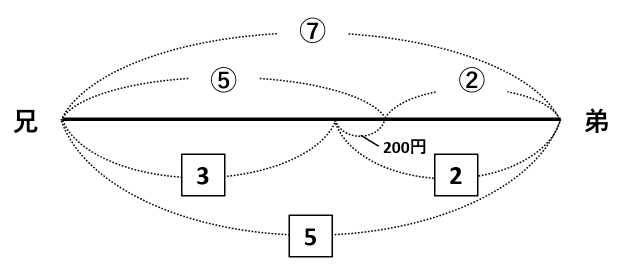
線分図の真ん中にやりとりしたお金を書くとわかりやすいよ！
下の図のように、2人の所持金の和である⑦と5が同じ長さなので、⑦と5の最小公倍数の
にそろえます。
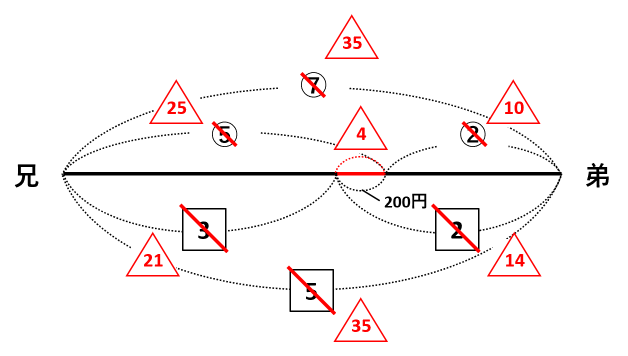
⑦を5倍したので、他の○の比も5倍しました。また、5を7倍したので、他の□の比も7倍しました。
赤い線分に注目して、
＝200円なので
＝200÷4＝50円です。兄のもとの所持金は
なので、50×25＝1250円が答です。
別解（比を最小公倍数にそろえる解き方）
2人の所持金を2本の線分図で表してみます。
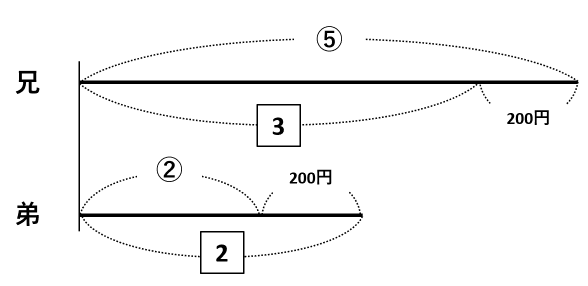
下の図では、3と2を最小公倍数の6にそろえました。
上の線分は、3を2倍したので、⑤と200円も2倍しました。一方、下の線分は、2を3倍したので、②と200円も3倍しました。
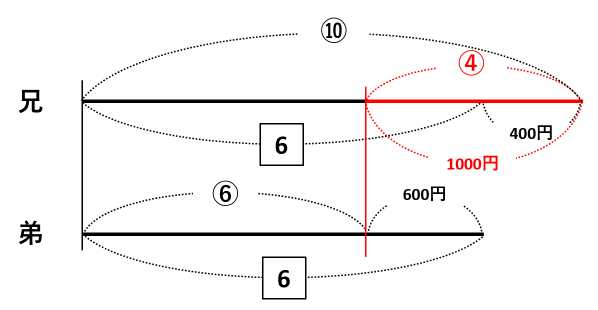
赤い線分に注目して、⑩－⑥＝④、400＋600＝1000円なので、④＝1000円です。したがって、①＝1000÷4＝250円とわかりました。
兄のもとの所持金は⑤なので、250×5＝1250円が答です。
最小公倍数を使いこなそう
倍数算では、和や差、○や□の比を最小公倍数にそろえることで、問題を解く手がかりをつかめます。
倍数算に限らず、最小公倍数を利用して解く特殊算は他にもあります。たとえば、消去算のコツは、最小公倍数にそろえて消去することです。また、仕事算では、全体の仕事量を日数の最小公倍数にすると解きやすくなります。
このように便利な最小公倍数を使いこなせるようになると、算数が楽しくなるはずです。
コメント