割合や比の応用問題である「相当算」の中には、問題文が長く複雑で、やや難しいものもあります。今回は、そんな難問をわかりやすく解説します。
相当算の基本は以下の記事を参照してください。

式を作って逆算で解いてみよう
計算力に自信のある受験生のために、全体のあめ玉を□個として式を作り、逆算で□を求める方法を紹介します。
全体のあめ玉を□個とします。
「太郎君が全体の4割より5個多くとりました」から、残りのあめ玉は□×0.6ー5(個)です。
「次郎君が残りの6割より5個多くとりました」から、残りのあめ玉は(□×0.6ー5)×0.4ー5(個)です。
「三郎君がとった分は全体の2割になりました」から、三郎君がとったあめ玉は□×0.2個です。
次郎君がとった後の残りのあめ玉と三郎君がとったあめ玉の個数は同じなので、式は(□×0.6ー5)×0.4ー5=□×0.2となります。
(□×0.6ー5)×0.4ー5=□×0.2
□×0.24ー2ー5=□×0.2
□×0.24ー□×0.2=2+5
□×0.04=7
□=7÷0.04=175
全体のあめ玉が175個とわかったので、太郎君、次郎君、三郎君がとったあめ玉の個数を求めていきます。
太郎君は175×0.4+5=75(個)、次郎君は(175ー75)×0.6+5=65(個)、三郎君は175ー75ー64=35(個)です。
線分図と消去算で解いてみよう
式を作って計算で解くのを難しく感じる受験生は、線分図を描いてみるとよいでしょう。
問題文には太郎君、次郎君、三郎君の3人が登場します。
まず、3本の線分を描いて、問題文の中にある数字を書きこんでいきます。
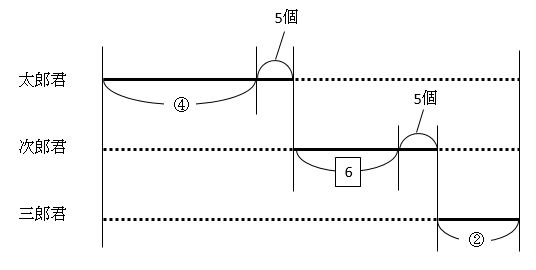
線分の上にはあめ玉の個数、下には割合を書きこみました。
割合は、小数や分数に直さず、歩合をそのまま使っています。歩合は、もとにする量を10として考えます。
太郎君と三郎君は、「全体」がもとにする量なので、割合を〇で囲みました。次郎君は、「残り」がもとにする量なので、割合を□で囲みました。

もとにする量が異なる割合は、〇や□を使って区別することが大切なんだ!
次に、わかるところをどんどん埋めていきます。
⑩から④と②を引いた④と、10から6を引いた4を線分図に書き足しました。
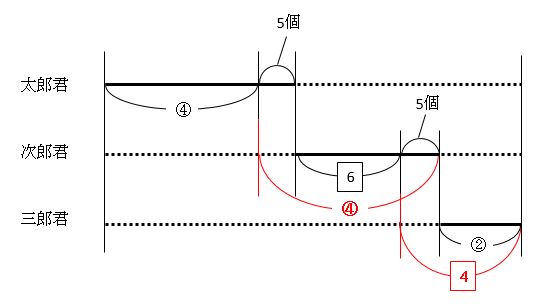
さらに、線分図を見て、式を作れないかを考えます。同じ長さの線分を探すのがポイントです。
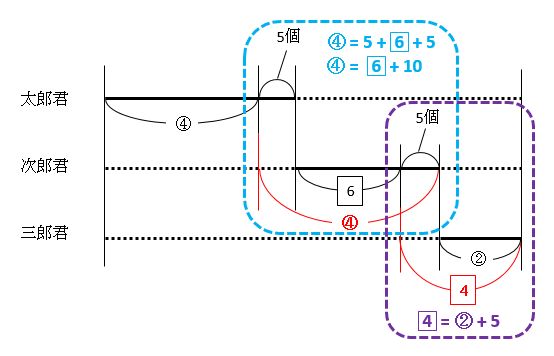
点線で囲った部分から、次の2つの式を作れます。
④=6+10 … ア
4=②+5 … イ
このような2つ以上の式から①や1を求めるのが「消去算」です。消去算では、リンゴとミカンのそれぞれの値段や、大人と子どものそれぞれの入園料などを求める問題が有名です。

この消去算が相当算でも役立ちます。実際に計算してみましょう。
ア全体を2倍します。
8=④+10 … ウ
アをウに代入します。
8=(6+10)+10 (← ④を6+10に書きかえました)
8-6=2=20
1=10

加減法や代入法を使って、○か□のどちらかを消去するのよ!
最後に、太郎君、次郎君、三郎君がとったあめ玉の個数を求めます。
次郎君 … 6+5=10×6+5=65
三郎君 … 4-5=10×4-5=35
太郎君 … ④+5=②×2+5=35×2+5=75
したがって、太郎君75個、次郎君65個、三郎君35個です。
線分図と消去算を使いこなそう
相当算では線分図がとても役に立ちます。さらに消去算も使いこなせれば鬼に金棒です。
逆算が苦手な受験生は、線分図と消去算で解く方法にもチャレンジしてみてください。
トップ画像=Pixabay



コメント
わかりやすかったです。
お役に立ててよかったです!