食塩水の濃度(濃さ)の問題では、「天秤図」と呼ばれる図がよく使われます。
本記事では、さまざまな濃度問題を天秤図で解いていきます。
濃度の異なる2種類の食塩水を混ぜ合わせる問題
問題文の数字を天秤に描き込んでいきます。
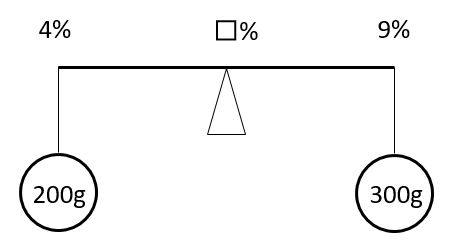
天秤図では、腕の左端には一番薄い濃度を、右端には一番濃い濃度を、中央の支点にはこれらの濃度の間にある濃度を書きます。
例題1では、混ぜた後の食塩水は9%よりも薄くなるので、求める濃度(□%)が支点になります。
食塩水の重さが分かっているので、重さの比を図に書き込みます。その後、重さの比の逆比を腕に書き足します。
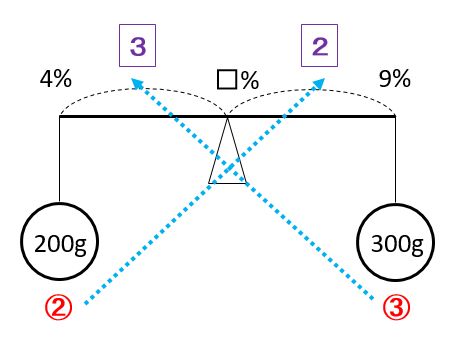
上の天秤図より、3は、9-4=5(%)を5つに分けたうちの3つ分です。したがって、3=5÷5×3=3(%)なので、□=4+3=4+3=7(%)です。
食塩や水を加える問題
天秤図では、食塩は100%の食塩水、水は0%の食塩水と考えます。このことをふまえて、例題2の天秤図を描くと次の通りです。
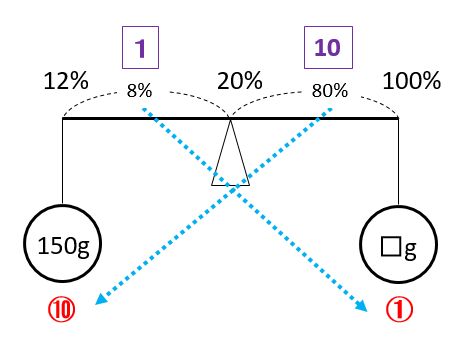
これより、加えた食塩の重さは、□=150÷10=15(g)です。
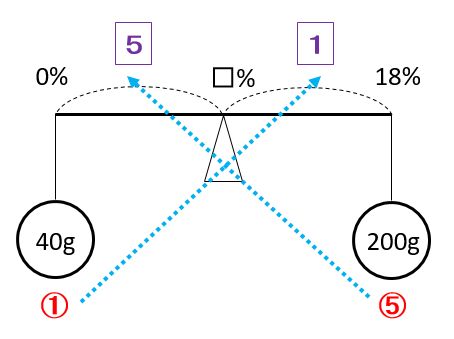
上の天秤図より、□=18÷6×5=15(%)です。
食塩や水の扱い方が分かれば、基礎の基礎である問題にも天秤図を使えます。
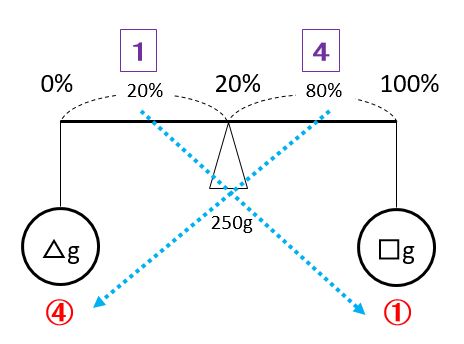
水△gと食塩□gを合わせると250gになります。上の天秤図より△:□=4:1なので、□=250÷5=50(g)です。

【例題4】は、250×0.2=50(g)ですぐに食塩の重さを求められる。天秤図を使うとかえってめんどくさい。でも、「食塩水のどんな問題にも天秤図が使える」ということがわかったよ。
水を蒸発させる問題
食塩水から水を蒸発させると、蒸発前の食塩水よりも蒸発後の食塩水の方が濃くなります。
蒸発問題では、天秤の左端に蒸発した水、中央に蒸発前の食塩水、右端に蒸発後の食塩水を書きます。
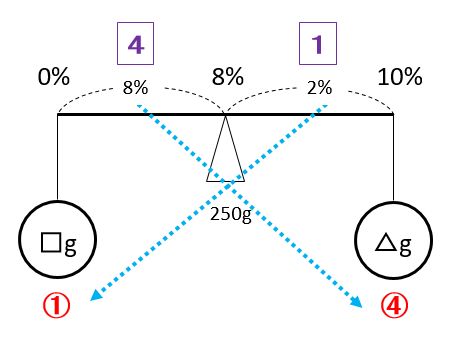
水□gと食塩△gを合わせると250gになります。上の天秤図より□:△=1:4なので、□=250÷5=50(g)です。

蒸発後の食塩水は、蒸発前と比べて、水の量だけ減って食塩の量は変わらないから、濃くなるのね。天秤図では「蒸発した水+蒸発後の食塩水=蒸発前の食塩水」という考え方を使うのよ。
こぼした後水を加える問題
食塩水の一部をこぼした後、残りの食塩水に水を加えると、こぼす前の食塩水よりも水を加えた後の食塩水の方が薄くなります。
こぼした後水を加える問題では、天秤の左端に加えた水(こぼした食塩水と重さが同じ)、中央に水を加えた後の食塩水(こぼす前の食塩水と重さが同じ)、右端にこぼした後に残っている食塩水(こぼす前の食塩水と濃度が同じ)を書きます。
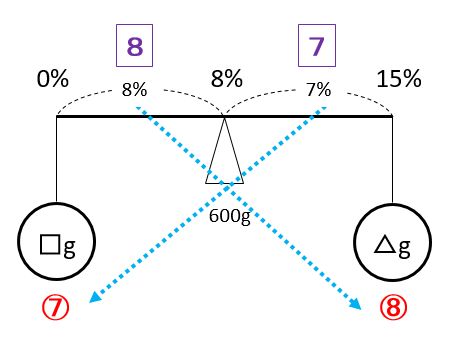
水□gと食塩水△gを合わせると600gになります。上の天秤図より□:△=7:8なので、□=600÷15×7=280(g)です。
加えた水の重さとこぼした食塩水と重さは同じなので、答は280gです。
食塩水をやりとりする問題
食塩水をやりとりする問題では、天秤のどこにどんな数を書けばいいかが分かれば難しくありません。また、このタイプの問題では、天秤図をいくつも描く必要があります。
(1)「はじめAの食塩水50gをBに入れてよくかき混ぜた後」
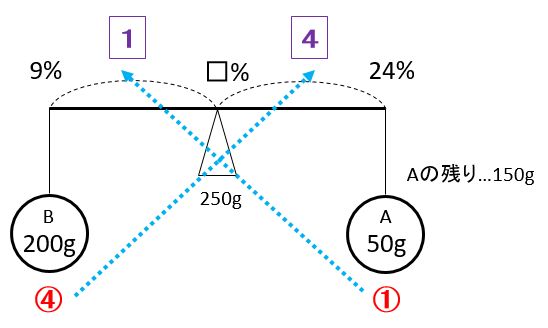
1=(24-9)÷5=3(%)なので、□=9+1=9+3=12(%)です。したがって、12%の食塩水が250gできたことになります。また、Aは150g残っていることもメモしておきましょう。
(2)「その食塩水50gをCに入れてよくかき混ぜ」
「その食塩水」は、(1)でできた12%の食塩水です。
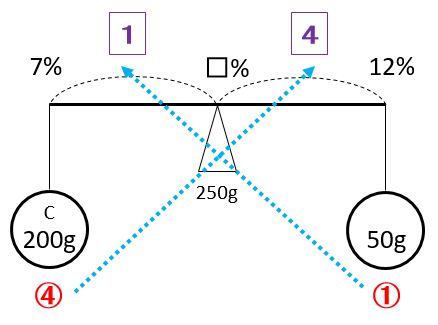
1=(12-7)÷5=1(%)なので、□=7+1=7+1=8(%)です。したがって、8%の食塩水が250gできたことになります。
(3)「最後にその食塩水50gをAに入れてよくかき混ぜました」
「その食塩水」は、(2)でできた8%の食塩水です。また、Aの重さは、(1)で残った150gです。
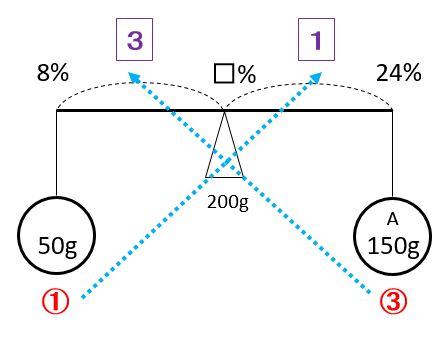
3=(24-8)÷4×3=12(%)なので、□=8+3=8+12=20(%)です。
便利な天秤図に頼るのは危険?
天秤図は、面積図で逆比を使う考え方から誕生しました。「天秤の腕の長さ=濃度」「おもり=濃度の異なる2種類の食塩水の重さ」とすることで、濃度問題をパズル的に解けるようになります。

天秤図は、食塩水の濃度問題だけでなく、平均算やつるかめ算などでも使えるので便利です。
しかし、逆比を理解した上で使わないと、「天秤図を使えば、理由は分からないけれども、答だけは出せる」状態になって、算数が伸び悩みます。
便利だからといって天秤図に頼るのは危険です。
トップ画像=Pixabay




コメント
一番初めにある天秤図の説明で、「左端には濃い濃度、右端には薄い濃度」ではなく、「左端には薄い濃度、右端には濃い濃度」ではございませんでしょうか
?
間違いのご指摘ありがとうございます。
早速修正いたしました。