割合や比の応用問題に「相当算」があります。
相当算とは、ある数がわかっているとき、割合や比をヒントにしてわからない数を求める計算です。
今回は分数の割合を含む相当算を解説します。
式を作って逆算で解いてみよう
計算力に自信のある中学受験生は、はじめに入っていた水の量(全体の水の量)を□Lとして式を作り、逆算で□を求めてしまうのが楽で速いです。
実際に式を作っていきましょう。
はじめに入っていた水の量(全体の水の量)を□Lとします。
「全体の\(\frac{1}{3}\)より10L多く水を出して」から、残っている水の量を□で表します。出した水の量が全体の\(\frac{1}{3}\)だけなら、残っている水の量は全体の\(\frac{2}{3}\)で□×\(\frac{2}{3}\)(L)です。ここからさらに10L多く水を出しているので、残っている水の量は□×\(\frac{2}{3}\)ー10(L)です。
「次に残りの\(\frac{1}{2}\)を出したら」から、出した水の量が残りの\(\frac{1}{2}\)なので、さらに残っている水の量は残りの\(\frac{1}{2}\)で(□×\(\frac{2}{3}\)ー10)×\(\frac{1}{2}\)(L)です。
「20Lの水が残りました」から、(□×\(\frac{2}{3}\)ー10)×\(\frac{1}{2}\)(L)が20Lだとわかるので、(□×\(\frac{2}{3}\)ー10)×\(\frac{1}{2}\)=20という式が完成しました。あとは、逆算で□を求めるだけです。
(□×\(\frac{2}{3}\)ー10)×\(\frac{1}{2}\)=20
□×\(\frac{2}{3}\)ー10=20÷\(\frac{1}{2}\)=40
□×\(\frac{2}{3}\)=40+10=50
□=50÷\(\frac{2}{3}\)=50×\(\frac{3}{2}\)=75
計算の結果□=75になったので、はじめに入っていた水の量は75Lです。
線分図を描いて解いてみよう
式を作って逆算で解くのが難しいと感じる受験生は線分図を描いて解いてみましょう。
多くの問題集では、線分図に「全体の\(\frac{1}{3}\)より10L多く水を出して」を書き込むとき、全体を1、出した水を\(\frac{1}{3}\)としています。しかし、分数の割合のままだと計算が面倒になりがちです。

分数の割合のままで線分図を描くとどうなるかは、以下の記事を参照してね。
わかりやすさを求めるのなら、分数の割合を整数の比で表すことをおすすめします。
「全体の\(\frac{1}{3}\)より10L多く水を出して」の「\(\frac{1}{3}\)」は「3つに分けたうちの1つ」なので、全体を③、出した水を①とします。
同じく「残りの\(\frac{1}{2}\)を出したら」の「\(\frac{1}{2}\)」は「2つに分けたうちの1つ」なので、残りを2、出した水を1とします。
「全体の\(\frac{1}{3}\)」と「残りの\(\frac{1}{2}\)」は、それぞれもとにする量が違います。そこで、比をそれぞれ○と□で分けます。

もとにする量が違う比は○や□などで区別することはとても大切だよ!
これらの比と10L、20Lを書き込んだ線分図は以下の通りです。
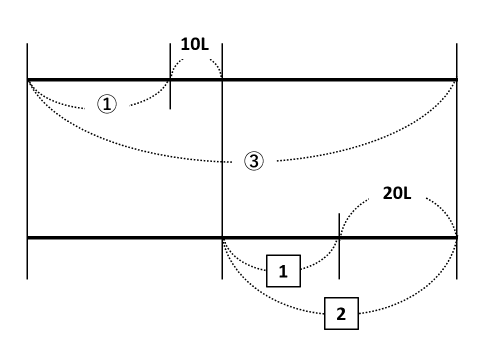
線分図のわかるところをどんどん埋めていきます。
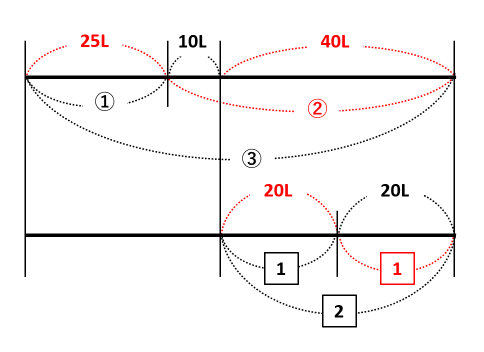
1=20Lなので2=40Lです。
この40Lと10Lを合わせて②=50Lです。
①=50÷2=25Lなので③=25×3=75Lとなり、はじめに入っていた水の量が75Lだとわかります。
分数の割合を整数の比に書きかえよう
多くの中学受験生が、分数の割合が苦手なために相当算でつまずきます。
そんな受験生は分数の割合を整数の比に書きかえてみましょう。そして、これらの比を線分図に書き込んで、わかるところをどんどん埋めていきましょう。
そうすれば面倒な計算をしなくても答が出ます。



コメント