いくつかわからない数があるとき、式を作ってこれらの数を求めるのが「消去算」です。
消去算は中学数学で学ぶ「連立方程式」の小学生バージョンといわれます。「連立方程式は難しい」と思われがちですが、実は簡単です。
そんな消去算の代表的な解き方を2つ紹介します。
加減法で解いてみよう
【例題1】では、ナスの本数が2本でそろっています。
消去算では、【例題1】のナスのように個数がそろっているものを消すのがポイントです。「消去算」という名前の中に、「消去=消し去る」という言葉が入っている理由です。
今回はナスを消去します。消し方を考えるために、まずは下の図を見てください。
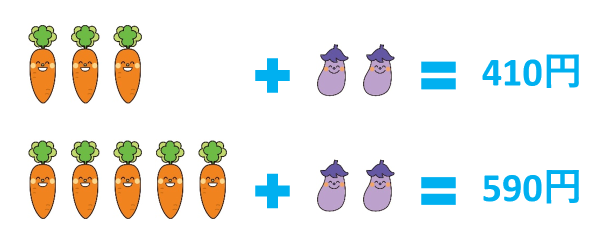
上の式と下の式を見比べて、「どうすればナスが消えるかな?」と考えましょう。
式同士を引けば、ナスを消去できることがわかりましたか?
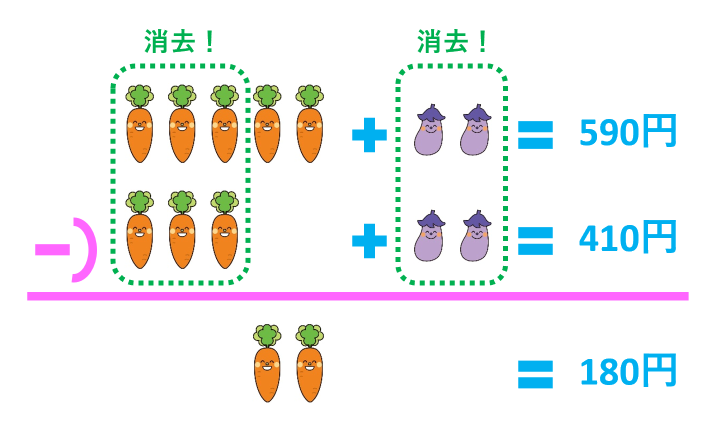
ニンジンの本数と代金の多い方(下の式)から少ない方(上の式)を引きました。
ナスだけでなく、ニンジン3本も消えて、代金も590-410=180円となり、ニンジン2本が180円だとわかりました。したがって、ニンジン1本は180÷2=90円です。
ニンジン1本が90円なので、ニンジン3本で270円です。上の式のニンジン3本を270円で置きかえて、ナス2本は410-270=140円です。したがって、ナス1本は140÷2=70円です。
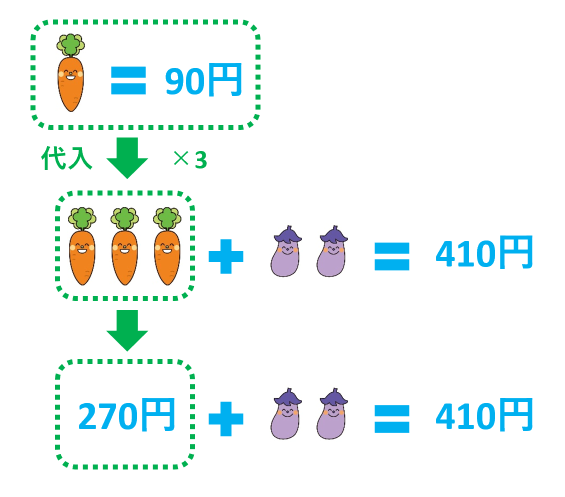
ニンジン3本を270円で置きかえましたが、このことを「ニンジン3本に270円を代入した」といいます。代入とは、置きかえることです。
ここまでで見たように、式同士を足したり引いたりして個数がそろっているものを消す方法を「加減法」といいます。
加減法をするのに絵を描くのは大変なので、普通は次のように書きます。
ニンジン1本の値段を「ニ」、ナス1本の値段を「ナ」とします。
ニ×3+ナ×2=410 …(ア)
ニ×5+ナ×2=590 …(イ)
(イ)ー(ア)より、
ニ×2=180
ニ=180÷2=90
ニ=90を(ア)に代入して、
90×3+ナ×2=410
ナ=(410-270)÷2=70
したがって、ニンジン1本が90円、ナス1本が70円
個数を最小公倍数にそろえよう
リンゴ1個の値段を「リ」、ミカン1個の値段を「ミ」とします。
リ×4+ミ×7=760 …(ア)
リ×8+ミ×5=980 …(イ)
困ったことに、(ア)と(イ)でリンゴもミカンも個数がそろっていません。
こういうときは、式を何倍かして、リンゴかミカンの個数をそろえます。
(ア)×2より、リ×8+ミ×14=1520 …(ウ)
これでリンゴの個数がそろったので、加減法でリンゴを消去できます。
(ウ)ー(イ)より、
ミ×9=540
ミ=540÷9=60
ミ=60を(ア)に代入して、
リ×4+60×7=760
ミ=(760-420)÷4=85
したがって、リンゴ1個が85円、ミカン1個が60円
ボールペン1本の値段を「ボ」、鉛筆1本の値段を「え」とします。
ボ×3+え×2=540 …(ア)
ボ×5+え×3=870 …(イ)
(ア)と(イ)の両方を何倍かして、ボールペンか鉛筆の本数をそろえます。
鉛筆の2本と3本を最小公倍数の6本にそろえるのが簡単です。
(ア)×3より、ボ×9+え×6=1620 …(ウ)
(イ)×2より、ボ×10+え×6=1740 …(エ)
これで鉛筆の本数がそろったので、加減法で鉛筆を消去できます。
(エ)ー(ウ)より、
ボ=120
ボ=120を(ア)に代入して、
120×3+え×2=540
え=(540-360)÷2=90
したがって、ボールペン1本が120円、鉛筆1個が90円
【例題3】は、ボールペンを15本にそろえても解けます。また、鉛筆を12本、18本、…などにしても、計算が面倒になるだけで、解けなくなるわけではありません。
【例題2】や【例題3】では、式を何倍かして個数をそろえました。個数をそろえるときは、最小公倍数にそろえるのがおすすめです。
代入法で解いてみよう
【例題4】ニンジン3本とナス2本で410円、ニンジン5本とナス2本で590円です。ニンジン1本はナス1本より20円安く買えます。ニンジン1本、ナス1本の値段はそれぞれいくらですか。
ニンジン1本の値段を「ニ」、ナス1本の値段を「ナ」とします。
ニ×3+ナ×2=410 …(ア)
ニ=ナ+20 …(イ)
「ニンジン1本はナス1本より20円安く買えます。」を式にすると(イ)になります。ニンジンとナスのどちらが安い(高い)のかを考えて、20円を足すのか引くのかを判断しましょう。
【例題4】のように、等号(=)をはさんで、わからない数(ここではニンジンとナスの値段)がわかれているときは、置きかえることを考えましょう。この置きかえが「代入法」です。
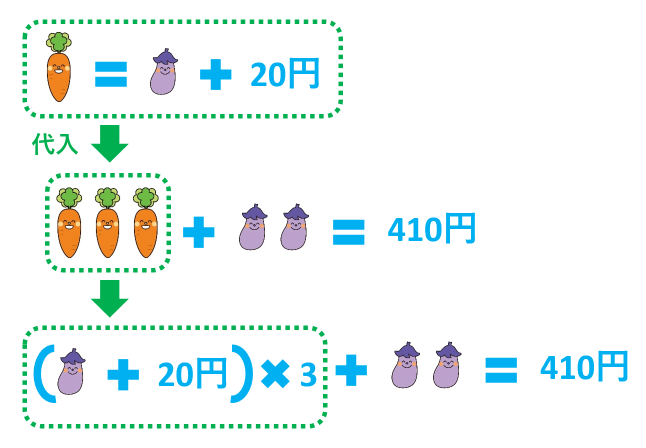
(イ)を(ア)に代入して、
(ナ+20)×3+ナ×2=410
ナ×3+60+ナ×2=410
ナ×5=410-60=350
ナ=350÷5=70
ナ=70を(ア)に代入して、
ニ×3+70×2=410
ニ=(410-140)÷3=90
したがって、ニンジン1本が90円、ナス1本が70円

(イ)を(ア)に代入するとき、ナ+20に( )を付けるのは、どうしてですか?

ナ+20でひとまとまりなので、「ナと20を分けてはいけません」という意味で( )を付けるんだ。

( )を付けないと、ナ+20×3+ナ×2=410ですね。これだと、ナ=(410-60)÷3=116.66…となって、ナス1個の値段が整数じゃなくなっちゃいます。

( )を付けることで、3をナにも20にもかけることになるんだ。分配法則を使って計算しようね。
消去算は他の特殊算でも使える
多くの中学受験生は、塾でサラッとしか習わない消去算を大切だとは思っていません。
それにもかかわらず、消去算はつるかめ算やニュートン算などの特殊算でも使える便利な道具です。消去算を使いこなせれば、さまざまな文章題を力ずくで解けます。
計算が得意な受験生は、消去算を練習しておくとよいでしょう。
次の質問に答えましょう。(解答例は最後のページにあります)
① 消去算では、式を2つ作った後、何をしますか。
② 代入とは何をすることですか。
③ 消去算で式を何倍かするのはどうしてですか。




コメント