【過不足算】面積図を描ければ余りや不足を足すか引くかで悩まない！

何個かのものを何人かにわけるとき、ものがあまったり不足したりすることがあります。このあまりや不足の個数をヒントに人数やもの全体の個数を求める問題が「過不足算」です。

多くの中学受験生が過不足算で「あまりや不足を足すの？引くの？」で混乱します。しかも、がんばって計算して数値を出したのに、その数値が何なのか分からなくなって、余計な計算をして不正解になります。

そんな受験生におすすめなのが面積図です。

あまりと不足の問題

過不足算で面積図を描くときは、縦に1人あたりの個数、横に人数を書くとよいでしょう。

【例題1】では、長方形の縦に子ども1人あたりがもらえるあめ玉の個数、横に子どもの人数□人を書きます。

わかりやすいように、あめ玉の個数の面積図を描き、それとは別に8個ずつ配る場合と5個ずつ配る場合を描いてみました。赤い部分がそれぞれあまりと不足の個数です。

8個ずつ配った場合、4個不足します。このとき、配ろうとしたあめ玉の個数は実際のあめ玉の個数より多いので、左の長方形は真ん中の長方形より大きくなります。

同じように、5個ずつ配った場合、26個あまります。このとき、配ろうとしたあめ玉の個数は実際のあめ玉の個数より少ないので、右の長方形は真ん中の長方形より小さくなります。

以上を面積図で表すと、次の通りです。

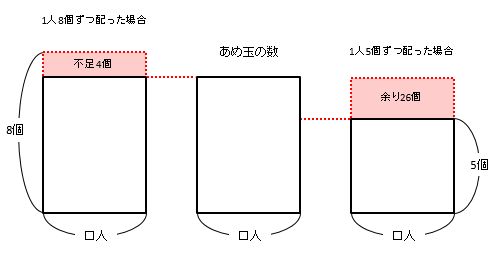
これら3つの長方形を重ね合わせます。

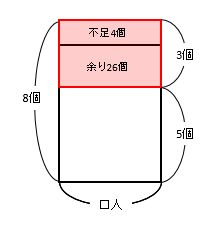
4＋26＝30個の長方形を見て、3×□＝30から□＝30÷3＝10人が答です。

シイタケくん

【例題1】は子どもの人数を求めるだけなので、ここで終わりだよ。もしあめ玉の個数まで求める場合は、8×10ー4か5×10＋26を計算して76個になるね。

「あまりと不足は足す」を暗記しなくても、面積図を正しく描ければ、あまりや不足を足すのか引くのかは自然とわかります。