【時計算】長針と短針が作る角度？速さの応用問題は追い越しの旅人算

問題演習コーナー

【問題】9時と10時の間で、時計の長針と短針が作る角の大きさについて、次の問いに答えなさい。

(1) 9時30分のとき、小さい方の角の大きさを求めなさい。

(2) 長針と短針の作る角の大きさが120°になるのは9時何分ですか。

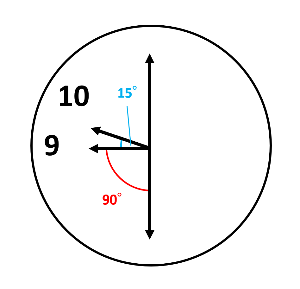
下の図から90°＋15°＝105°が答えです。

ちなみに、短針は30分で毎分0.5°×30分＝15°動きます。

1回目と2回目に120°になる時刻をそれぞれ求めます。

① 1回目に120°になるまでの時間

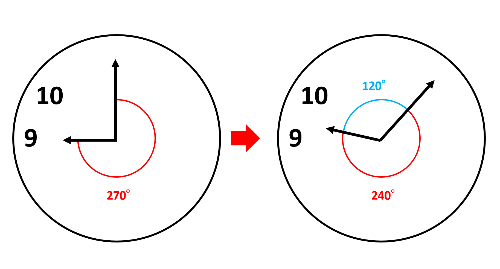
下の図から、9時で長針と短針は270°離れていて、毎分\(\frac{11}{2}\)°ずつ近づいていって、ある時刻で240°になります。270°から240°まで30°を縮めたことになるので、30°÷毎分\(\frac{11}{2}\)°＝5\(\frac{5}{11}\)分です。

② 2回目に120°になるまでの時間

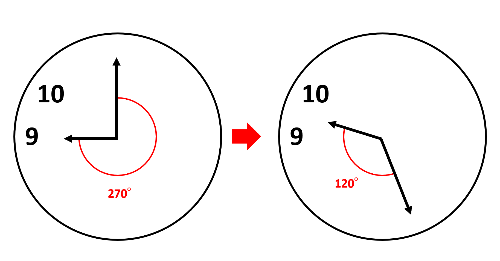
下の図から、9時で長針と短針は270°離れていて、毎分\(\frac{11}{2}\)°ずつ近づいていって、ある時刻で120°になります。270°から120°まで150°を縮めたことになるので、150°÷毎分\(\frac{11}{2}\)°＝27\(\frac{3}{11}\)分です。

①②より、求める時刻は9時5\(\frac{5}{11}\)分と9時27\(\frac{3}{11}\)分です。

エリンギ先生

特に指示がない場合、長針と短針の作る角の大きさが120°になる時刻をすべて書かないといけないから、注意しましょう。

・時計算で使う\(\frac{11}{2}\)はどのような数ですか。

（例）長針の角速度である毎分6°と短針の角速度である毎分0.5°の差です。

トップ画像＝写真AC