旅人算などの速さの応用問題は、ダイヤグラムから相似な三角形を見つけると簡単に解ける場合があります。
本記事では、相似を利用して旅人算を図形的に解く方法を紹介します。
ダイヤグラムと相似を利用して旅人算を解こう
【例題】A、B2つの駅の間を、一定の速さで往復する電車があります。この電車は、駅では6分間停車します。太郎君は、電車がA駅を出発してから10分後に自転車でB駅を出発して、線路沿いの道をA駅まで時速12kmの速さで向かいました。下の図は、このときの様子を表したグラフです。
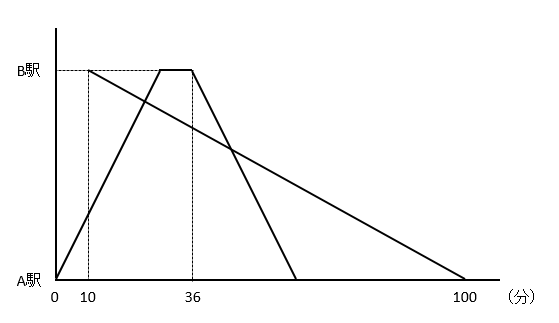
次の問いに答えなさい。
(1) 電車の速さは、時速何kmですか。
(2) 太郎君が電車とすれちがった地点は、A駅から何kmのところですか。
(3) 太郎君が電車に追いこされた地点は、A駅から何kmのところですか。
(1)の解き方（電車の速さを求める）
(1)では電車の速さを求めます。
問題文には「この電車は、駅では6分間停車します」とあるので、電車はA駅からB駅までの距離を36分－6分＝30分（＝\(\frac{1}{2}\)時間）で走ることがわかります。
一方、太郎君は、時速12kmの速さで、A駅からB駅までの距離を100分－10分＝90分（＝\(\frac{3}{2}\)時間）で走りました。したがって、A駅からB駅までの距離は、時速12km×\(\frac{3}{2}\)時間＝18kmです。
以上より、電車の速さは、18km÷\(\frac{1}{2}\)時間＝時速36kmです。
□分＝\(\frac{□}{60}\)時間だから、30分＝\(\frac{30}{60}\)時間＝\(\frac{1}{2}\)時間よ。「分」を「時間」に変換するときは60で割ることになるわ。その理由については以下の記事を参考にしてね。
(2)の解き方（すれちがった地点の距離を求める）
(2)では、太郎君が電車とすれちがった地点の距離を求めます。
旅人算の出会い算ですが、相似な三角形を利用して図形的に解くこともできます。2つの解き方を紹介します。
旅人算（出会い算）として解く
下の図のように、電車と太郎君の隔たり（距離）を一辺とする三角形に着目しましょう。
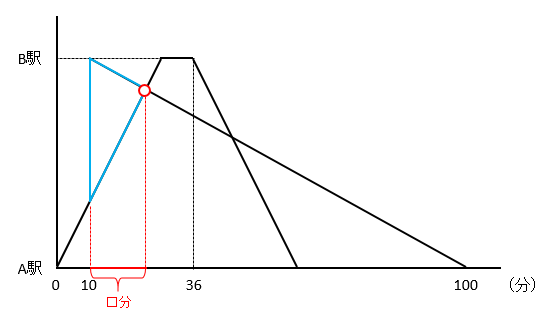
まずは、電車と太郎君の隔たり（距離）を求めます。電車は10分間で、時速36km×10分＝時速36km×\(\frac{1}{6}\)時間＝6kmの距離を移動しているので、電車と太郎君の隔たり（距離）は、18km－6km＝12kmです。
次に、電車と太郎君の間の距離が1時間でどのくらい縮まるかを考えます。1時間で電車が36km進むと、太郎君は電車に12km近づきます。したがって、電車と太郎君の速さの和を考えます。
これより、□分＝12km÷（時速36km＋時速12km）＝\(\frac{1}{4}\)時間となり、この時間で電車がA駅から進んだ距離は時速36km×\(\frac{1}{4}\)時間＝9kmです。したがって、求める距離は、9km＋6km＝15kmです。
相似な三角形を利用して解く
下の図のように、ABとDEが平行なので三角形ABCと三角形DECが相似です（ちょうちょ）。
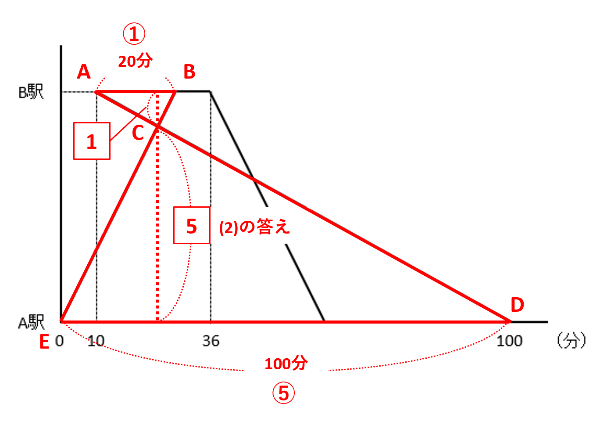AB＝36分－10分－6分＝20分、DE＝100分なので、AB：DE＝20：100＝1：5です。三角形ABCの底辺をAB、三角形DECの底辺をDEとすると、2つの三角形の高さの比も1：5です。したがって、求める距離は18km×\(\frac{5}{1＋5}\)＝15kmです。
(3)の解き方（追いこされた地点の距離を求める）
(3)では、太郎君が電車に追いこされた地点の距離を求めます。
(2)と同じように、2つの解き方を紹介します。
旅人算（追い越し算）として解く
下の図のように、電車と太郎君の隔たり（距離）を一辺とする三角形に着目しましょう。
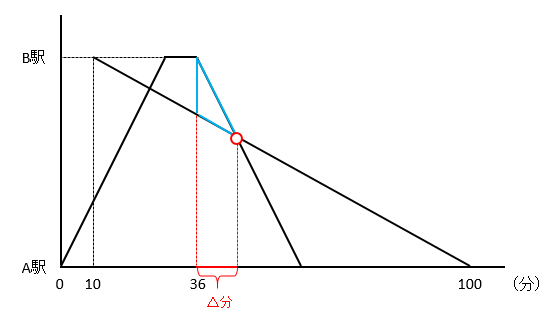
まずは、電車と太郎君の隔たり（距離）を求めます。この隔たりは、太郎君が36分－10分＝26分（\(\frac{13}{30}\)時間）で進んだ距離に等しいので、時速12×\(\frac{13}{30}\)時間＝5.2kmです。
次に、電車と太郎君の間の距離が1時間でどのくらい縮まるかを考えます。1時間で電車が36km進むと、太郎君は電車から12km離れます。したがって、電車と太郎君の速さの差を考えます。
これより、△分＝5.2km÷（時速36km－時速12km）＝\(\frac{13}{60}\)時間となり、この時間で電車がB駅から進んだ距離は時速36km×\(\frac{13}{60}\)時間＝7.8kmです。したがって、求める距離は、18km－7.8km＝10.2kmです。
相似な三角形を利用して解く
下の図のように、ABとDEが平行なので三角形ABCと三角形DECが相似です（ちょうちょ）。
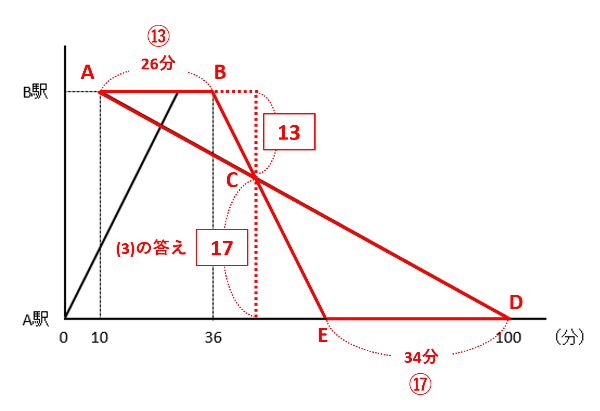
AB＝36分－10分＝26分、DE＝100分－36分－30分＝34分なので、AB：DE＝26：34＝13：17です。三角形ABCの底辺をAB、三角形DECの底辺をDEとすると、2つの三角形の高さの比も13：17です。したがって、求める距離は18km×\(\frac{17}{13＋17}\)＝10.2kmです。
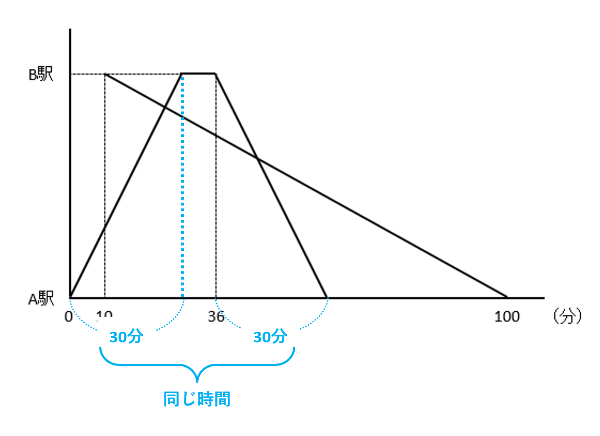
問題文に「一定の速さで往復する電車」と書かれているから、電車がA駅を出発してからB駅に到着するまでの時間と、B駅を出発してからA駅に到着するまでの時間は、どちらも30分だよ。
普段の勉強でダイヤグラムを描いて慣れよう
旅人算などの速さの応用問題では、【例題】のようなダイヤグラムを与えられなくても、自分でダイヤグラムを描いて相似を利用すると簡単に解けることが少なくありません。中学受験生は、速さを得意にするためにも、普段の勉強でダイヤグラムを描いて慣れておくとよいでしょう。
トップ画像＝写真AC
コメント