速さの応用問題に「流水算」があります。その中でも、比を利用して解く問題は複雑で、多くの中学受験生が苦手とします。
そんな受験生泣かせの問題をダイヤグラムで解いていきましょう。
エンジン故障の問題を解いてみよう
【例題】は文章が長いですが、状況を理解できますか?
船のエンジンが途中で壊れて30分間動かなくなったとき、この船は川の同じ地点にとどまっていたわけではないことに注意しましょう。つまり、エンジンが故障したとき、船は川に流されて下流へ移動しました。
このことをふまえてダイヤグラムを描くと次の通りです。
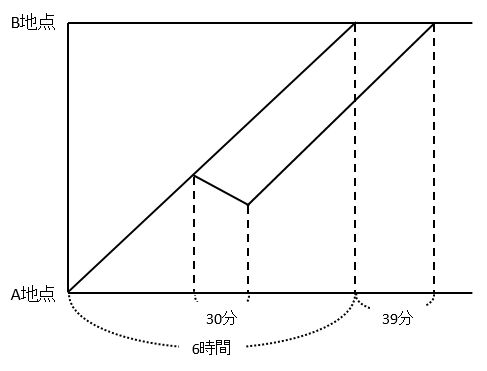
船の速さについて、静水時の速さが一定なので、右上がりの2本の直線は平行です。また、この2直線によってできる時間の差は、6時間39分-6時間=39分です。
ダイヤグラムを描いたら、まずが三角形を探しましょう。39分を活かす形で補助線を引くと、下の図の赤い三角形を作れます。
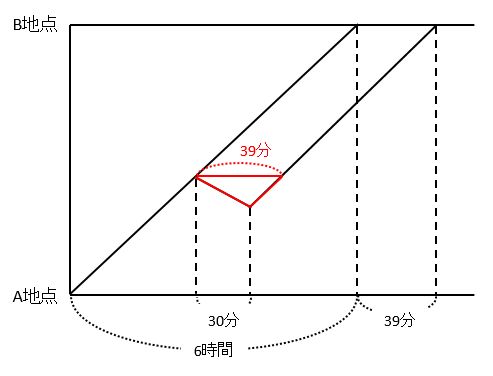
39-30=9(分)で船が進んだ道のりを求めます。
問題文から、船が48km上るのに6時間かかっているので、船の上りの速さは48km÷6時間=毎時8kmです。したがって、毎時8km×\(\frac{9}{60}\)時間=\(\frac{6}{5}\)kmを求められました。
この\(\frac{6}{5}\)kmを30分で移動する速さが川の流れの速さなので、\(\frac{6}{5}\)km÷\(\frac{30}{60}\)時間=時速2.4kmです。
また、船の静水時の速さは「船の上りの速さ+川の流れの速さ」なので、毎時8km+毎時2.4km=毎時10.4kmとなります。
【別解】川の流れの速さを逆比で求める
道のりが一定なので、時間と速さは逆比です。
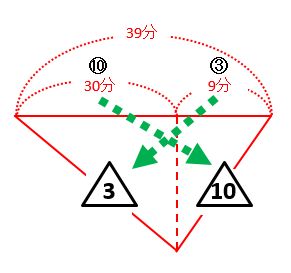
時間の比=30分:9分=10:3から、川の流れの速さと船の上りの速さの比が3:10とわかりました。
川の流れの速さは、船の上りの速さの\(\frac{3}{10}\)倍で毎時8km×\(\frac{3}{10}\)=毎時2.4kmとなります。
また、船の静水時の速さは毎時8km+毎時2.4km=毎時10.4kmです。

速さの応用問題でダイヤグラムが役立つ
【例題】のような複雑な速さの問題を解きとき、ダイヤグラムがとても役に立ちます。
上位校志望の中学受験生は、普段の問題演習で積極的にダイヤグラムを描いて、ダイヤグラムを利用した解き方に慣れておくとよいでしょう。




コメント