電車には長さがあります。この長さを考えなければならない速さの問題を「通過算」といいます。
通過算には、電柱やトンネルなどを通過する問題や2台の電車が出会ったり追い越したりする問題があります。「問題ごとに解き方を覚えなければならない」と思っている中学受験生がいます。しかし、通過算では、「道のり=速さ×時間」の関係がわかっていて、正しく図を描ければ、解き方の丸暗記は必要ありません。
いくつかの例題を使って、通過算の考え方をていねいに解説します。
動くものと動かないものの通過算を考えよう
【例題1】長さ200m、秒速25mの電車が走っています。このとき、次の問いに答えなさい。
(1) この電車が電柱の前を通過するのにかかる時間は何秒ですか。
(2) この電車が750mの陸橋を渡り終えるまでにかかる時間は何秒ですか。
まず、(1)と(2)の違いを考えましょう。電柱も陸橋も動きません。一方、電柱は横の長さを考えませんが、陸橋は横の長さが750mです。つまり、(1)と(2)の違いは、横の長さがあるかないかという点だけです。したがって、同じ考え方で(1)も(2)も解けます。
次に、「通過する」や「渡り終える」の意味を理解しましょう。(1)では、電車の先頭が電柱に重なった後、同じ電車の最後尾が電柱に重なることを「通過する」といいます。(2)も同じように考えます。
ここまで理解した上で、実際に問題を解きましょう。
(1)の解説(電柱の前を通過する)
(1)の問題文から、電車と電柱の関係を図にすると、下のようになります。わかりやすいように、電車の先頭をとがらせました。
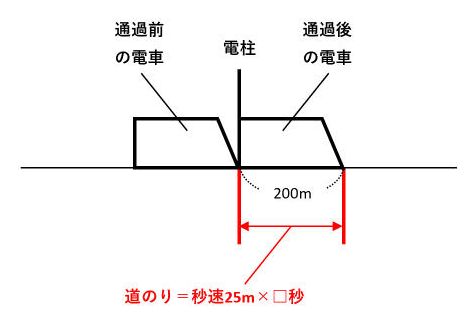
通過算では、電車の先頭か最後尾に注目するのがポイントです。今回は、先頭が動いた道のりを考えました。
求める時間を□秒とすると、「道のり=速さ×時間」なので、道のりは25×□になります。これが電車の長さ200mと等しいので、25×□=200です。したがって、□=200÷25=8(秒)が答です。

電柱にも横の長さはあると思うんですが……。

現実世界では、確かに電柱にも横の長さはある。でも、算数の文章題では、「電柱には横の長さが無い」という暗黙の了解があるんだ。だから、電柱を描くときは、長方形ではなく縦線にしてね。
(2)の解説(陸橋を渡り終える)
(1)と同じように、(2)も図を描きます。
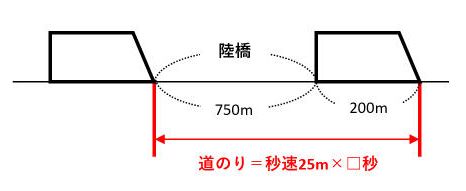
求める時間を□秒とすると、道のりは25×□です。これが電車の長さと陸橋の長さの和200+750=950(m)と等しいので、25×□=950です。したがって、□=950÷25=38(秒)が答です。
動くもの同士の通過算を考えよう
【例題2】長さ350m、秒速25mの電車Aと、長さ250m、秒速15mの電車Bが走っています。このとき、次の問いに答えなさい。
(1) AとBが出会ってからすれちがい終わるまでにかかる時間は何秒ですか。
(2) AがBに追いついてから追い越し終わるまでにかかる時間は何秒ですか。
例題2は例題1と違って、電車Aも電車Bも動きます。動くもの同士の通過算も、図を描いて考えれば簡単です。
(1)の解説(出会ってからすれちがう)
出会った瞬間とすれちがい終わった瞬間の図をそれぞれ描いて、情報を書き加えます。
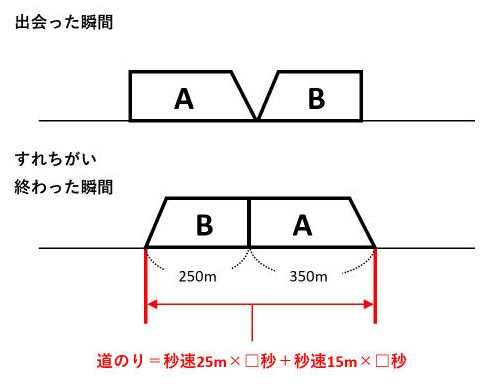
求める時間を□秒とすると、AとBが進んだ道のりの和は25×□+15×□=(25+15)×□です。これが2台の電車の長さの和350+250(m)と等しいので、(25+15)×□=350+250です。したがって、□=(350+250)÷(25+15)=15(秒)が答です。
図を描いて考えると、2台の電車の長さの和を2台の速さの和で割る理由が理解しやすくなります。
(2)の解説(追いついてから追い越す)
(1)と同じように、追いついた瞬間と追い越し終わった瞬間の図をそれぞれ描きます。
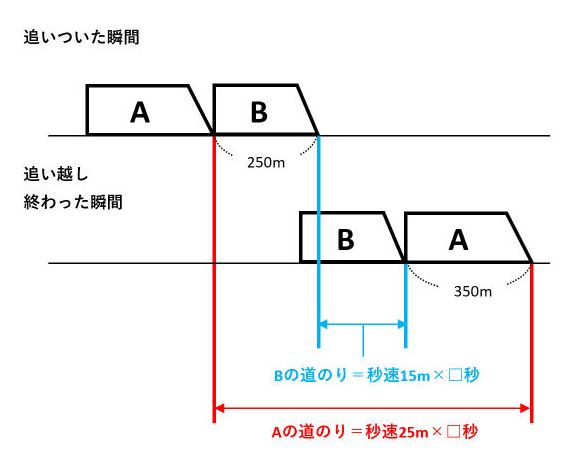
この図からどのような式を作るかで悩むかもしれません。そんなときは、「350mと250mを上手く使えないかな?」と考えて、図をじっくり眺めてみましょう。
Aの道のりからBの道のりを引くと、2台の電車の長さの和になっていることに気づきましたか?
このことに気づいたら、後は簡単です。求める時間を□秒とすると、AとBが進んだ道のりの差は25×□-15×□=(25-15)×□です。これが2台の電車の長さの和350+250(m)と等しいので、(25-15)×□=350+250です。したがって、□=(350+250)÷(25-15)=60(秒)が答です。
「通過算の追い越しでは、電車の長さの和を速さの差で割る」と丸暗記するのではなく、図を描いて「なぜそうなるのか?」を理解することが大切です。

考え方は旅人算と同じだよ。ただ、旅人算では動く人やものの横の長さを考えなかったけど、通過算では横の長さを考えるんだ。
簡単な通過算で図を描いてみよう
通過算は、速さの応用問題でも簡単な方です。状況をイメージしやすく、ダイヤグラムを描く必要もないからです。
だからといって、「2台の電車が出会う問題で時間を求めるときは、2台の長さの和÷速さの和」のように丸暗記していると、少しひねられたり、比がからんだりするだけで、手も足も出なくなります。
「簡単だから解き方を暗記しよう」ではなく、「簡単だからこそ図を描いて、どうしてそうなるのかを理解しよう」という姿勢で勉強することをおすすめします。
次の質問に答えましょう。(解答例は最後のページにあります)
① 電車が電柱の前を通過する問題と陸橋を渡る問題は、どこに違いがありますか。
② 「電車が電柱の前を通過する」とはどういうことですか。
③ 通過算では何に注目しますか。




コメント