【等差数列】公式を導いてみよう！n番目の数も和も簡単に求められる

数字が並んだ列のことを「数列」といいます。中でも、一定の数を次々に加えていった（引いていった）数列が「等差数列」です。たとえば、2、5、8、11、…は、初めの数が2、加える数が3の等差数列です。初めの数は「初項（しょこう）」、加える数は「公差（こうさ）」と呼ばれます。

今回は、等差数列の性質を考えながら、n番目の数や和を求める公式を導いてみます。

n番目の数と和を求める公式を導こう

例題1の数列は、初めの数が3、加える数が4の等差数列です。等差数列は、数直線を描いてみるとイメージしやすくなります。

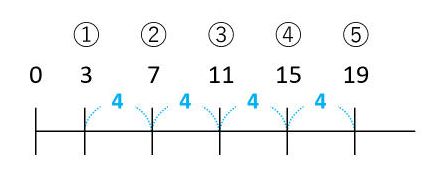
n番目の数を求めよう

(1)では、がんばって4を足していけば、25番目の数を求めることができます。しかし、何度も何度も4を足していくのは大変です。そこで、3、7、11、15、19について、「初めの数に4をいくつ足しているのか？」を考えて、規則性を探ってみることにします。等差数列に限らず、数列の問題を考えるときは、いくつかの数から規則性を探ることが大切です。

このように書き出してみると、初めから数えて25番目の数が3＋4×24＝99であるとわかります。

書き出した結果から、等差数列のn番目の数を求める公式を導けます。（n番目の数を「一般項（いっぱんこう）」といいます）

この公式は覚えておいた方が便利です。公式を使えば、25番目の数＝3＋4×（25－1）＝99となります。

何番目にあるかを求めよう

(2)は、公式を使えばあっという間に答を求められます。255が初めから数えて□番目にあるとすると、3＋4×（□－1）＝255です。したがって、□＝（255－3）÷4＋1＝64（番目）が答です。

次のように数直線を使えば、公式を使わなくても解けるでしょう。

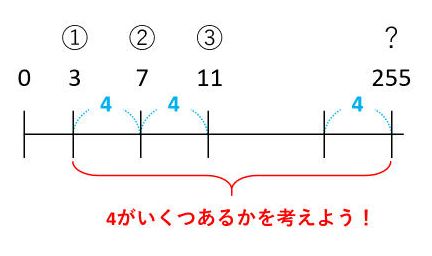
3から255の間に4がいくつあるかを考えると、（255－3）÷4＝63です。255は、初め（1番目）の数である3に4を63個足したので、64番目の数です。

和を求めよう

(3)は、1番目から64番目までの数を全て足さなければなりません。どのようにして和を求められるのかを、3＋7＋11＋15＋19＝55を使って考えてみましょう。

等差数列の和を求める場合、数列を逆順に並べるのがコツです。3＋7＋11＋15＋19を逆順に並べると19＋15＋11＋7＋3です。3＋7＋11＋15＋19と19＋15＋11＋7＋3を次のように足します。

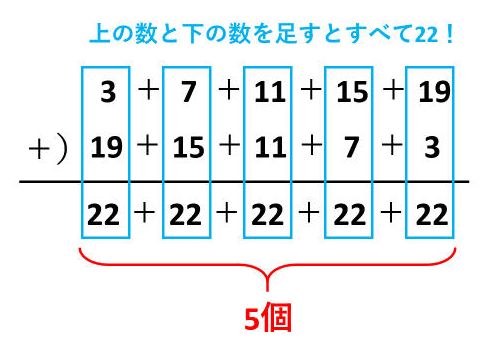
数列を縦に足していくと22が5個できます。この22は「初めの数＋終わりの数」です。また、22×5＝（3＋7＋11＋15＋19）＋（19＋15＋11＋7＋3）＝（3＋7＋11＋15＋19）×2なので、3＋7＋11＋15＋19＝22×5÷2＝55となります。数列の和2つ分を1つにするために「÷2」をします。

この結果から、等差数列の和を求める公式を導けます。

この公式を使えば、(3)の答は（3＋255）×64÷2＝258×32＝8256です。

エノキさん

258×64をしてから÷2をするんじゃなくて、258÷2か64÷2を先にしてしまうと、計算が少し楽になるわ！

等差数列の公式を使いこなそう

等差数列の少しひねった問題にチャレンジしましょう。

(1)の解答（全部の個数を求める）

例題2の数列は、200から7を次々と引いていった等差数列です。しかし、例題1の「加える数」が「減らす数」になっているので、とまどうかもしれません。そこで、次のように、数列を逆順に並べてみましょう。

こうすれば、初めの数が3、加える数が7の等差数列と考えられます。

200が初めから数えて□番目にあるとすると、4＋7×（□－1）＝200です。したがって、□＝（200－4）÷7＋1＝29となり、全部で29個の数を並べたとわかります。

シイタケくん

初めの数が200、引く数が7の等差数列と考えて、200－7×（□－1）＝4とするのはどうですか？

エリンギ先生

もちろん正しい式だよ。ただ、（　）を外すと200－7×□＋7になって、中学数学の正負の数を学んだ後でないと、－7×（－1）＝＋7になる理由がわからないんじゃないかな？

エノキさん

A－□＝Bが□＝A－Bになることを利用して、7×（□－1）＝200－4にすれば、－7×（－1）＝＋7の計算は要らないですよね？

エリンギ先生

逆算（□を求める計算）が得意なら、そういう式変形をするのも有りだね。ただ、計算ミスをしないように注意する必要がある。逆順に並べる考え方は、計算に自信のない受験生におすすめなんだ。

(2)の解答（ちょうど真ん中の数を求める）

真ん中の数を求めるため、29÷2を計算すると、商が14、あまりが1です。この結果を図で表すと、次のようになります。

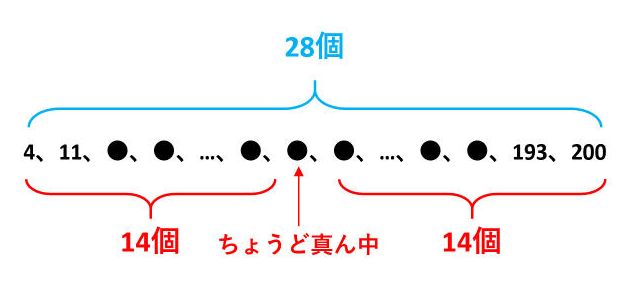
図より、ちょうど真ん中の数は初めから数えて15番目だとわかります。したがって、4＋7×（15－1）＝102が答です

等差数列の公式を導いてみよう

等差数列の公式は、ただ覚えるだけでなく、「どうしてそうなるの？」を理解するといいでしょう。そうすれば、試験本番で公式を忘れてしまってもあわてなくて済みます。

等差数列は高校数学でも登場します。そのときに、公式の成り立ちをしっかり理解した経験が必ず役に立ちます。