中学受験算数では、「速さ」がとても大切です。しかし、多くの受験生は、速さの問題を「みはじ」や「きはじ」などに当てはめて計算するだけで「理解した」つもりになっています。それでは、入試問題を解くのは難しいでしょう。
今回は、「『速さ』とは何か?」から始めて、簡単なダイヤグラム(進行グラフ)の読み取りまでの基礎を解説します。
「速さ」の意味をしっかり理解しよう
「速さ」は、単位時間あたりに進む道のり(距離)のことです。単位時間は「1時間」「1分間」「1秒間」のどれかです。
- 時速…1時間で進む道のり
- 分速…1分間で進む道のり
- 秒速…1秒間に進む道のり
時速を表すときは、「時速30km」「毎時30km」のように「時速」「毎時」をつけるか、「30km/時」「30km/h」と書きます。「/時」は「毎時」と読みます。「/(スラッシュ)」は「÷」なので、「km/時」は「km÷時間」という意味です。また、「/h」の「h」は「hour」(時間)の略です。
ちなみに、「時速30km」と「30km」はちがうので注意しましょう。単なる「30km」は、速さではなく道のりです。
同じように、分速は「分速40m」「毎分40m」「40m/分」「40m/min」(min=minute(分))と表せます。また、秒速は「秒速10m」「毎秒10m」「10m/秒」「10m/s」(s=second(秒))と表せます。

道のり・速さ・時間の関係を線分図で表そう
道のり・速さ・時間の関係について、「みはじ」や「きはじ」などの図で表されることがあります。この図を用いれば、「速さ=道のり÷時間」などの公式がパッとわかります。
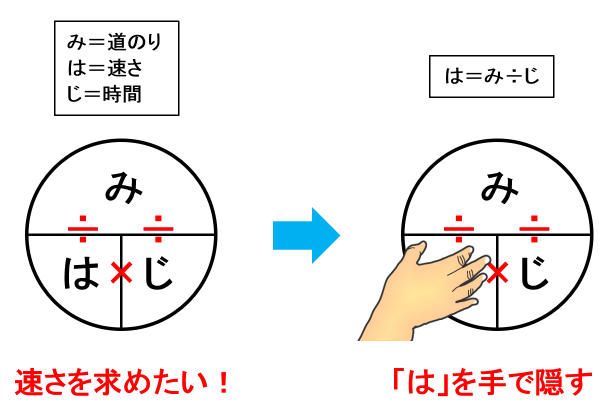
「みはじ」の図は一見すると便利です。しかし、これに頼っていると、速さの本当の姿がなかなか見えてきません。「みはじ」の図をどうしても使いたければ、速さをきちんと理解した後に使うようにしましょう。
そこで、「みはじ」の図に頼らないで、次の例題1を考えてみます。
【例題1】
(1) 時速40kmの自動車が3時間走ったときに進む道のりは□kmです。
(2) 320kmの道のりを4時間で走る電車の速さは時速□kmです。
(3) 840mの道のりを分速60mで歩くのにかかる時間は□分です。
速さが一定ならば、道のりと時間は比例する
速さが一定(同じ)ならば、道のりと時間は比例します。同じ速さで歩き続ける限り、歩く時間が2倍、3倍、4倍……になると、進む道のりも2倍、3倍、4倍……になります。これは感覚的にも理解できるでしょう。そして、この比例関係を表すのに役立つのが線分図です。
(1)の解説(道のりを求める)
時速が1時間で進む道のりを表していることをふまえて、線分図を描きます。
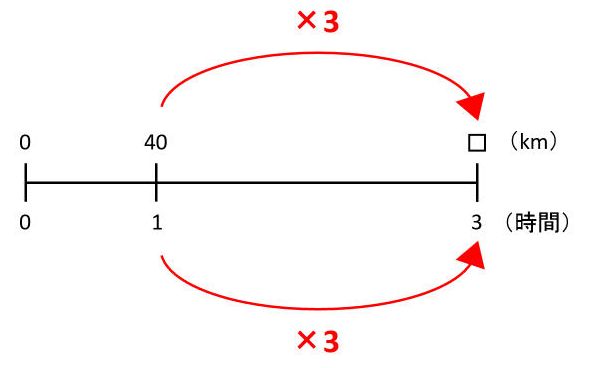
図を見て、時間が×3になっているので、道のりも×3します。したがって、□=40×3=120(m)です。「道のり=速さ×時間」になっています。
(2)の解説(速さを求める)
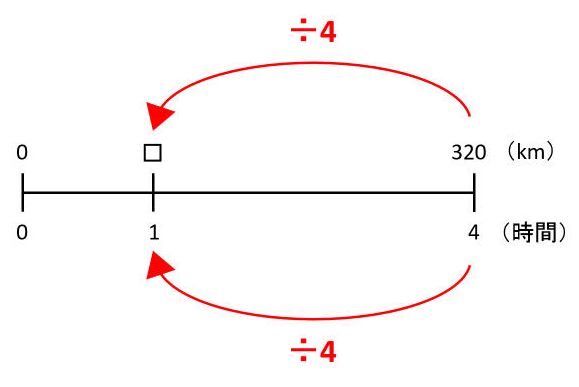
図を見て、時間が÷4になっているので、道のりも÷4します。したがって、□=320÷4=(時速)80(km)です。「速さ=道のり÷時間」になっています。
(3)の解説(時間を求める)

比例では、縦に並んだ数字にも規則性があります。このことに注目すると、60と1が÷60になっているので、840も÷60すると□を求められます。したがって、□=840÷60=14(分)です。「時間=道のり÷速さ」になっています。
線分図を描けば、速さを求めなくてよいこともある
線分図を描いて問題を解くことに慣れていると、次のような問題で、いちいち速さを求める必要がなくなります。
例題2同じ速さで走る自動車が3時間で160km進むとき、12時間では□km進みます。
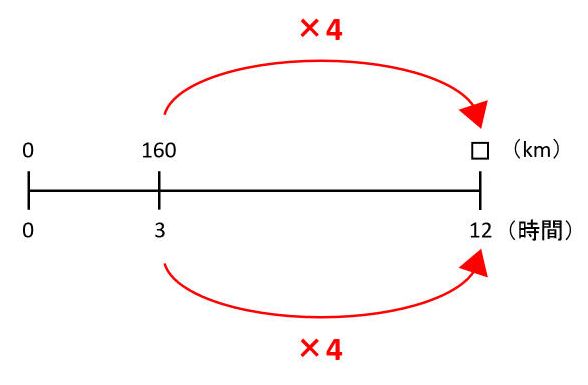
図を見て、時間が×4になっているので、道のりも×4します。したがって、□=160×4=640(km)です。
この問題では、「まずは速さを求めよう」と思って160÷3を計算すると、割り切れません。ここで混乱する受験生がいます。しかし、そもそも速さを求める必要はありません。計算する前に、図を描いて情報を整理することが大切です。
道のり・速さ・時間の関係を面積図で表そう
前ページでは、道のり・速さ・時間の関係を線分図で表しました。これを面積図で表すこともできます。「道のり=速さ×時間」なので、長方形の縦を速さに、横を時間に、面積を道のりにします。
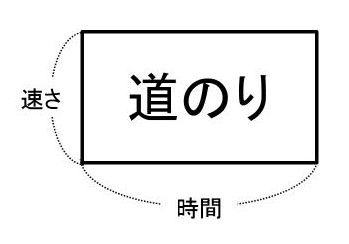
かけ算や割り算で表される関係は面積図で表すとわかりやすくなります。
道のり・速さ・時間の関係を面積図で覚えておけば、速さの三公式「道のり=速さ×時間」「速さ=道のり÷時間」「時間=道のり÷速さ」をわざわざ暗記する必要はありません。
そして、面積図は比例や反比例を理解するのにも役立ちます。たとえば、前ページで紹介した「速さが一定ならば、道のりと時間は比例する」というのも、面積図で考えれば明らかです。
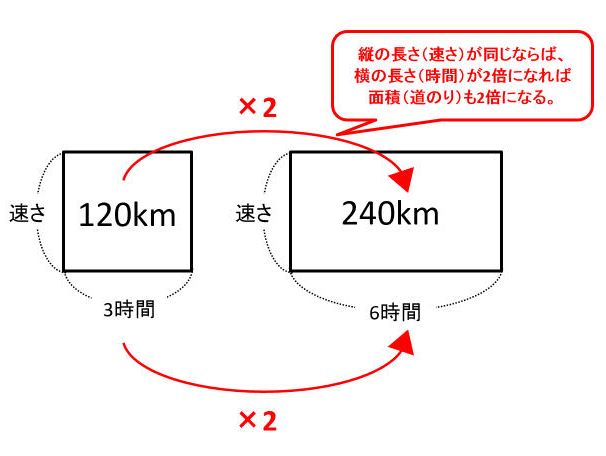
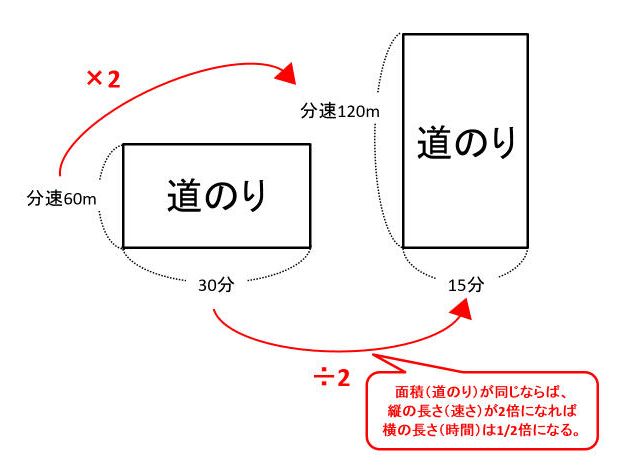
同じように考えれば、「時間が一定ならば、道のりと速さは比例する」とわかるはずです。逆に、「道のりが一定ならば、速さと時間は反比例する」ということも、面積図からわかるでしょう。

道のり・速さ・時間の関係を面積図で表す場合、縦を速さにしないといけないんですか?

縦を時間にしたからといって、まちがいというわけではない。でも、縦を速さにした方がいい。鶴亀算や平均などで面積図を描くとき、普通は縦を単位量あたりの大きさ(1に対応する数。「1匹の足は2本」「1個100円」など)にするよね。だから、道のり・速さ・時間の関係を面積図で表す場合も、単位時間あたりに進む道のりである速さを縦にした方が、他の特殊算と同じように考えられるメリットがあるんだ。

面積が道のりというのが、なかなか理解しにくいです。

これはもう、理解するとかしないとかではなく、受け入れるしかないことだよ。高校物理ではv-tグラフという、速さを縦軸(v)に、時間を横軸(t)にとったグラフを扱うけど、ここでも「面積=道のり」が出てくる。だから、今のうちに、道のりを面積で表すことに慣れていくといいんじゃないかな?
道のり・速さ・時間の関係をダイヤグラムで表そう
道のり・速さ・時間の関係を表すグラフをダイヤグラム(進行グラフ)といいます。ダイヤグラムから情報を読み取るためのコツを紹介します。
ダイヤグラムから情報を読み取ろう
たとえば、「太郎君が歩きと走りでA地点からB地点へ行きました」という状況をダイヤグラムで表してみます。
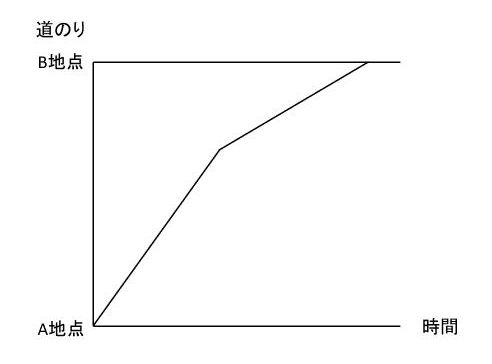
このダイヤグラムからは、大切な情報をたくさん読み取れます。読み取れる情報をすべて書き込むと次のようになります。
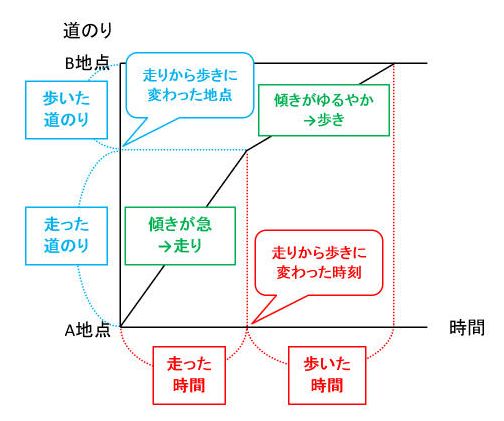
ダイヤグラムでは、直線の傾き(直線の斜め具合)で速さが表されます。傾きがゆるやかな直線と急な直線がある場合、急な方が速さは大きいとわかります。
ダイヤグラムは、斜めに傾いた直線の方に目が行ってしまいがちです。しかし、時間や道のりを読み取る場合は、横軸と縦軸の目盛りを見ます。縦軸だけを抜き出したのが、「状況図」と呼ばれる線分図です。
ダイヤグラムで特に大切なのは、直線の傾きが変わっている点です。この点が何を意味しているのかを正しく理解しましょう。上の図では、直線の傾きが変わっている点で太郎君が走りから歩きになったと考えられます。

塾の先生は、「小学生には難しいから、なるべくダイヤグラムを使わない方がいい」と言ってます。

もちろん、すべての問題でダイヤグラムを描く必要はないし、将来的にはダイヤグラムを使わない解き方も身に付けるべきだ。でも、「難しい」という理由だけでダイヤグラムを避けていると、入試本番でダイヤグラムが出てきたときに固まっちゃうよ。

「ダイヤグラムをわかってるけど、今回は使わない」と「ダイヤグラムがわからないから、今回も使えない」は別ってことですね。

「ダイヤグラムを使うな」と言う先生の中には、生徒にとって難しいからではなく、自分が生徒に理解させるのが難しいから、ダイヤグラムを嫌ってる人もいると思うよ。問題が複雑になればなるほどダイヤグラムが役立つし、最近の入試ではダイヤグラムを読み取る問題がよく出る。それなのに、教える側の都合でダイヤグラムを教えないのは最悪だ。
ダイヤグラムでは直角三角形を見つけよう
次の例題3にチャレンジしてみましょう。
【例題3】家から図書館までの途中に公園があり、その公園から図書館までは500m離れています。太郎君は9時に家を出て分速70mで歩き、途中の公園で10分休んだ後、図書館へ歩きました。このときの様子を表したのが下のグラフです。これについて、次の問いに答えましょう。
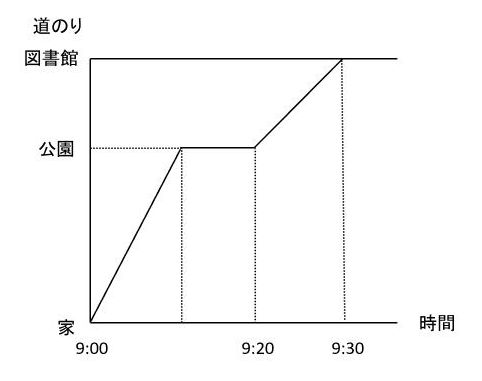
(1) 公園から図書館まで歩いたときの速さは分速何mですか。
(2) 家から図書館までは何km離れていますか。
ダイヤグラムが与えられる場合、まずは問題文から読み取れる情報(「500m」「分速70m」「10分」)をダイヤグラムに書き込みましょう。
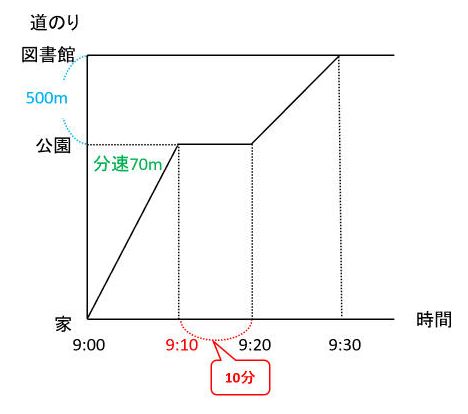
ここまで準備した上で(1)から問題を解いていきます。
(1)の解説(速さを求める)
ダイヤグラムでは、道のり・速さ・時間のうち2つの情報の分かっている直角三角形を見つけることが大切です。(1)では、9時20分から30分のところにある直角三角形に注目します。
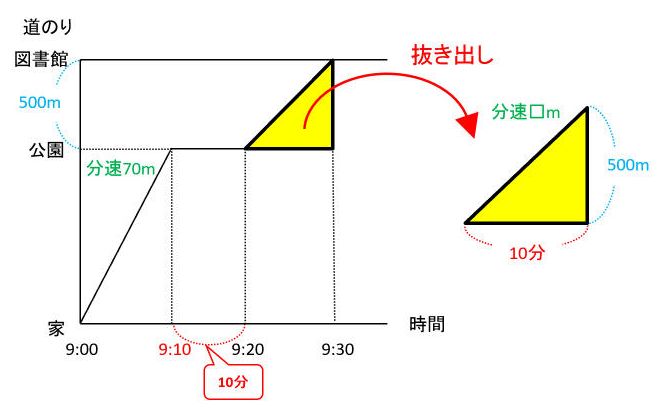
この三角形から、分かっている道のりと時間を使って速さ(図の□)を求めると、□=500÷10=(分速)50(m)が答です。
(2)の解説(道のりを求める)
(2)も、(1)と同じように考えて、9時から9時10分のところにある直角三角形に注目します。
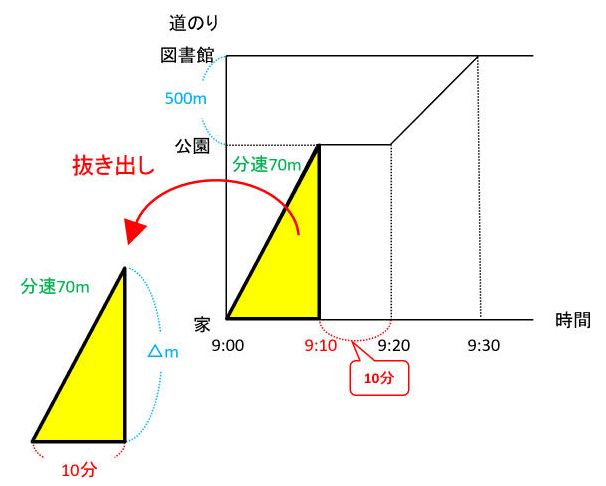
この三角形から、分かっている速さと時間を使って道のり(図の△)を求めると、△=70×10=700(m)です。これは家から公園までの道のりなので、家から図書館までの道のりは700+500=1200(m)です。
ダイヤグラムに慣れておこう
今回は道のり・速さ・時間の関係を線分図・面積図・ダイヤグラムの3つの図で表してみました。これらの図を使いこなせるようになると、速さの問題を解くのが楽しくなるはずです。
3つの図の中では、ダイヤグラムが特に大切です。速さと比の問題では、ダイヤグラムを図形として考えていきます。そのときまでに、ダイヤグラムから情報を読み取ったり、与えられた情報をダイヤグラムに表したりすることに慣れておきましょう。
次の質問に答えましょう。(解答例は最後のページにあります)
① 「時速」とは何ですか。
② 速さが一定(同じ)のとき、道のりと時間はどのような関係になっていますか。
③ 道のり・速さ・時間の関係を面積図で表すとき、それぞれは長方形のどこに対応しますか。
④ ダイヤグラムでは、何が速さを表しますか。
⑤ ダイヤグラムでは、どのような図形を見つけるといいですか。




コメント