【損益算】応用問題も簡単に解ける！仕入れ値・売上・利益を図にする

ある品物を仕入れて売ったときの利益を求める問題が「損益算」です。損益算の中でも、たくさんの品物を売るタイプの応用問題は「難しい」と思われがちです。

今回は【例題】を使って、損益算の応用問題のさまざまな解き方を紹介します。

□を求める計算で解いてみよう

計算力に自信のある中学受験生は、□を求める計算で解くのがよいでしょう。

たくさんの品物を売る場合、「売り上げの合計－仕入れ値の合計＝利益」の関係が成り立ちます。定価で売ったナシを□個として、この関係を□で表します。

売り上げの合計は、定価150円で□個売った合計金額なので、150×□円です。

仕入れ値の合計は、いたんでいた12個も含めて考えます。1個80円で□＋12（個）仕入れた合計金額なので、80×（□＋12）＝80×□＋960（円）です。

「売り上げの合計－仕入れ値の合計＝利益」にあてはめて、150×□－（80×□＋960）＝2400となります。（　）を外して、次のように計算します。

計算結果から、答は48個です。

エノキさん

（　）を外すとき、＋960が－960になるんですね！

エリンギ先生

その通り！もし（　）を外すときに＋と－でごちゃごちゃになるなら、「売り上げの合計＝仕入れ値の合計＋利益」の式を使おう。引き算がなければ、（　）を使う必要はないよ。

シイタケくん

「売り上げの合計＝仕入れ値の合計＋利益」にあてはめると、150×□＝80×□＋960＋2400です。

線分図で解いてみよう

計算で解くのが難しいのなら、線分図を描いてみましょう。

線分図では、仕入れたナシを□個として、この□個すべてが定価で売れたと考えます。

いたんでいた12個が定価で売れると150円×12個＝1800円です。

仕入れ値の合計と、仕入れたナシ□個すべてが定価で売れたときの売り上げの合計を線分図で表します。

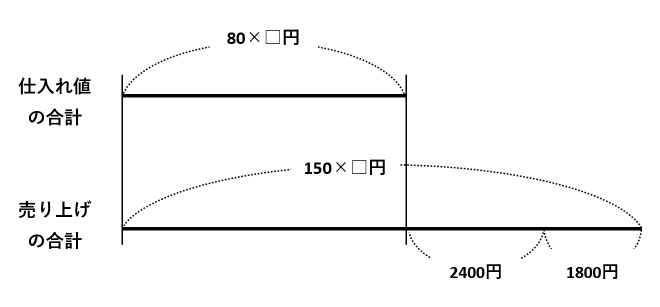
数字の分かっている線分（2400円＋1800円＝4200円）に注目します。この線分（下の図の赤い線分）を□で表すと、150×□円－80×□円＝70×□円です。

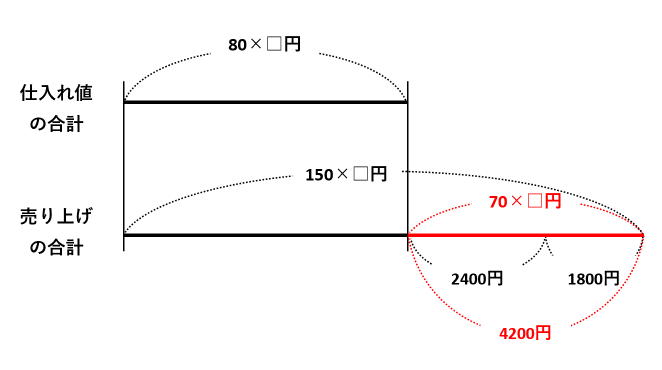
70×□＝4200なので、□＝4200÷70＝60（個）です。

60個は仕入れた個数なので、いたんでいた個数を引いて、仕入れた個数は60－12＝48（個）が答です。

シイタケくん

定価で売ったナシの個数を直接求められないんですか？

エリンギ先生

求められないことはないけれど、線分図で表すのは難しい。

エノキさん

そもそも、「仕入れたナシ□個すべてが定価で売れた」というのがひらめきません。

エリンギ先生

線分図が難しければ、面積図で表すとわかりやすいよ。面積図なら、定価で売ったナシを□個として考えられるんだ。

面積図で解いてみよう

【例題】には、「1個80円」「1個150円」という単位量あたりの大きさとこれらの個数があるので、問題文を面積図で表せます。面積図では、縦に単位量あたりの大きさを、横に個数を書くとよいでしょう。

定価で売ったナシの個数を□個として、面積図を描くと次の通りです。

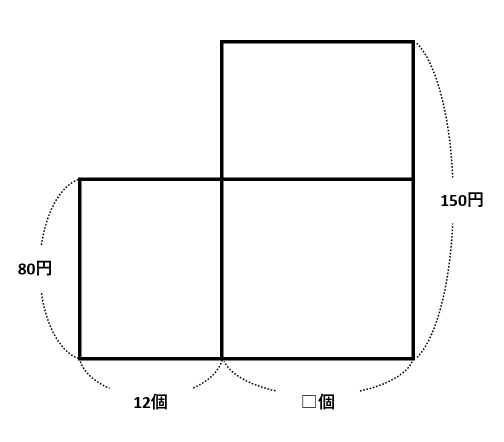
150－80＝70（円）を書きこみ、それぞれの四角形に①から③の番号を振ります。

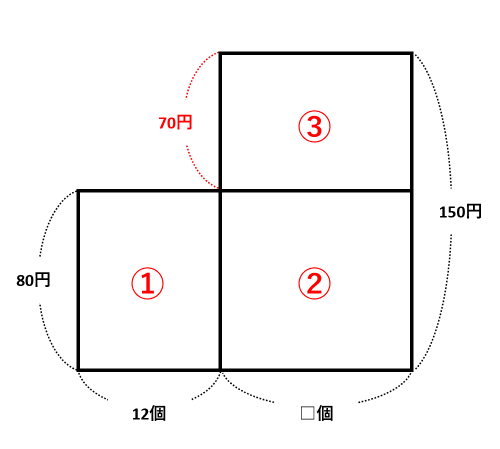
仕入れ値の合計は①と②の面積の和です。売り上げの合計は②と③の面積の和です。

「売り上げの合計－仕入れ値の合計＝利益」より、利益は（②と③の面積の和）－（①と②の面積の和）＝③－①と表せます。

シイタケくん

仕入れたナシがすべて売れたわけじゃないから、③は利益にならないよ！

エノキさん

売り上げの合計と仕入れ値の合計で②が共通なので、売り上げの合計から仕入れ値の合計を引くと、②が消えてしまうわ！

計算結果から、答は48個です。

仕入れ値・売上・利益を図にしよう

たくさんの品物を売るタイプの損益算は、仕入れ値の合計と売り上げの合計を図に表してみるとわかりやすくなります。このとき、線分図や面積図が役に立ちます。