中学受験算数で特殊算の入門といえば「和差算」です。多くの受験生が3年か4年で和差算に出会うでしょう。
今回は、中学受験算数の万能ツール「線分図」を使って和差算を解説します。
2つの数の和差算を考えよう
【例題1】大小2つの数があります。その和は12、その差は6です。2つの数は、それぞれいくつですか。
2つの数の和差算には次の公式があります。
(和+差)÷2=大きい数
(和-差)÷2=小さい数
この公式を覚えるだけでなく、「どうしてこうなるの?」をきちんと理解することが大切です。そうでないと、数が3つ、4つ……と増えたとき、手も足も出なくなります。
線分図を使って公式が正しいことを確かめよう
今回は、公式が正しいことを確認するため、中学受験の万能ツール「線分図」を使います。2つ以上の数の大小関係を理解するのに役立つのが線分図だからです。
実際に例題1を線分図で表すと、次の通りです。
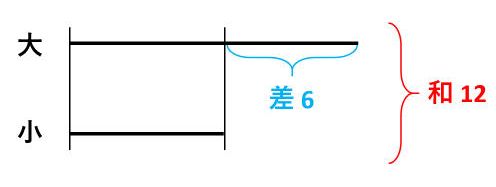
2つの数の和と差がそれぞれどこになるのかを理解しましょう。その上で、「和+差」と「和-差」を表すと、次のようになります。
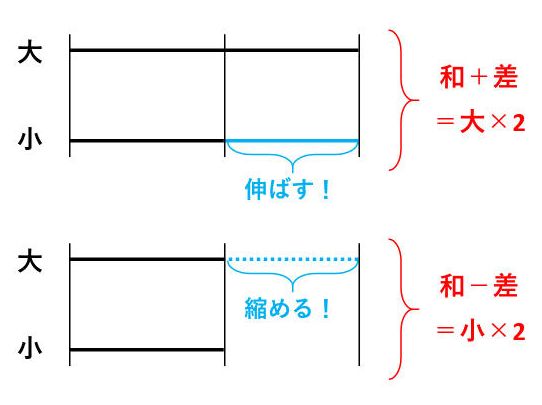
「和+差」は、小さい数を差の分だけ伸ばしたことになるので、「大きい数×2」になります。したがって、「(和+差)÷2=大きい数」が正しいとわかります。
一方、「和-差」は、大きい数を差の分だけ縮めたことになるので、「小さい数×2」になります。したがって、「(和+差)÷2=大きい数」も正しいとわかります。
公式が正しいことが確かめられたので、それぞれに数字を当てはめて例題1を計算しましょう。大きい数は(12+6)÷2=9で、小さい数は(12-6)÷2=3です。
線分図を見ながら□を含む式を作ろう
線分図を正しく描ければ、無理に公式を使わなくても問題を解くことができます。線分図のどこかの長さを□にし、□を含むイコール(=)の式を作って、逆算で□を求められるからです。
たとえば、小さい数を□にするなら、次のように線分図を描きます。
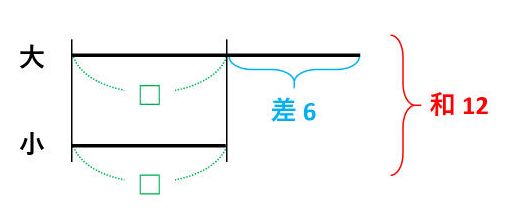
線分図に□が2つあるので□×2です。これに差の6を足せば和の12なので、□×2+6=12です。したがって、小さい数は□=(12-6)÷2=3で、大きい数は3+6=9です。
公式を使わなくても簡単に解けました。

大きい数を□にしちゃダメなんですか?

もちろんダメってことはないよ。大きい数を□にすると、小さい数は□を使ってどう表す?

小さい数は大きい数より6だけ小さいから□-6です。

その通り。だから、イコールの式は□+(□-6)=12になって、□=9を求められるんだ。

小さい数と大きい数のどっちを□にしたか、忘れないようにしないといけませんね!
3つの数の和差算を考えよう
線分図を使った考え方は、3つの数の和差算でもそのまま使えます。次の例題2を解いてみましょう。
【例題2】大中小3つの数があります。これらの和は35で、大と中の差は4、中と小の差は5です。それぞれの数を求めなさい。
【例題2】も【例題1】と同じように線分図を描くと、次の通りです。
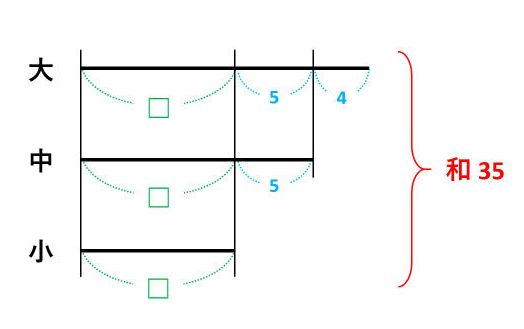
小を□として、線分図を見ながら式を作って、大中小の数を求めます。
□×3+5×2+4=35
□×3+14=35
小は、□=(35-14)÷3=7
中は、7+5=12
大は、7+5+4=16
万能ツール「線分図」に慣れよう
3つの数の和差算にも、公式らしいものがあります。しかし、その公式を一生懸命覚えようとするよりも、線分図を正しく描いてそこから式を作れるようにした方がよいでしょう。さらにいえば、2つの数の和差算でも、線分図を使いこなせれば、無理に公式を覚える必要はありません。
線分図は、中学受験算数全体で役に立つ万能ツールです。和差算を通して、その使い方に慣れましょう。
次の質問に答えましょう。(解答例は最後のページにあります)
① 線分図はどのようなときに役立ちますか。
② 公式を使わず、線分図を使って和差算を解く手順を説明しましょう。



コメント