三角形の面積比を考える場合、相似比を使えないなら、底辺比を使うのが定番です。
今回は、底辺比を使って面積比を考える問題をわかりやすく解説します。
高さが等しい三角形に注目しよう
複雑な問題にチャレンジする前に、次のことをしっかり理解しましょう。
たとえば、下の三角形を考えます。
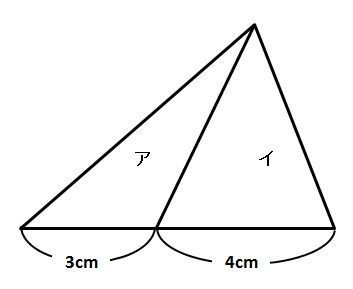
アとイの面積比を考えるとき、1本の補助線を引くのがコツです。
大きな三角形の頂点のうち、ア・イ両方の三角形の頂点が集まっている頂点から、向かい合う辺に垂直となる線を引きました。
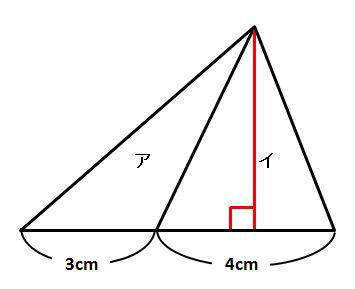
この補助線は、ア・イ両方の三角形の高さです。このことから、アとイは、高さが等しい三角形だとわかります。
アの面積は3×補助線の長さ×\(\frac{1}{2}\)、イの面積は4×補助線の長さ×\(\frac{1}{2}\)なので、面積比はア:イ=3×補助線の長さ×\(\frac{1}{2}\):4×補助線の長さ×\(\frac{1}{2}\)=3:4です。
したがって、高さの等しい三角形アとイの面積比は底辺比に等しいことがわかりました。
底辺比を利用して面積比を求めよう
「高さが等しい2つの三角形の面積比は底辺比に等しい」をふまえて、次の【例題】を解いてみましょう。
【例題】下の図のア~エの三角形は、それぞれ三角形ABCの面積の何倍ですか。ただし、辺上の点は、それぞれの辺を等しく分ける点です。
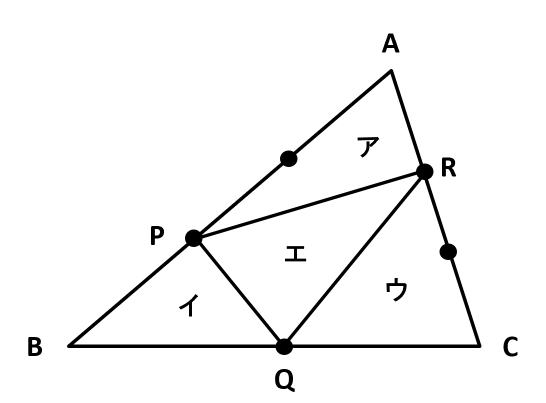
三角形アの面積から考えます。
下の図のようにPとCを結び、三角形ACPと三角形BCPに分割します。

余計な線のPQやQRを無視するとわかりやすいよ。
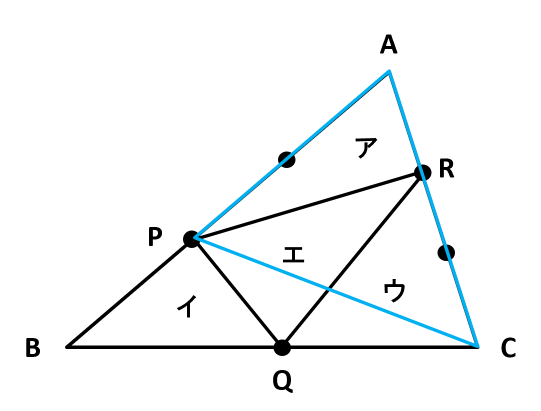
三角形ACPの底辺をAP、三角形BCPの底辺をBPとします。三角形ACPと三角形BCPの面積比は底辺比に等しいので、三角形ACP:三角形BCP=2:1です。
したがって、三角形ABCの面積を1とすると、三角形ACP=三角形ABC×\(\frac{2}{3}\)=1×\(\frac{2}{3}\)=\(\frac{2}{3}\)です。
同じように、三角形APRの面積を考えます。今度は三角形ACPに注目します。
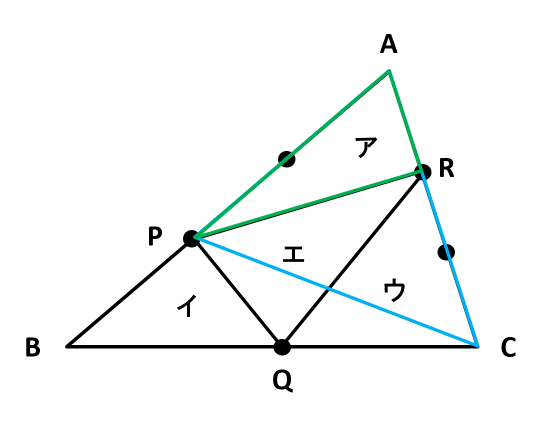
三角形APRの底辺をAR、三角形CPRの底辺をCRとすると、三角形APRと三角形CPRの面積比は底辺の比に等しいので、三角形APR:三角形CPR=1:2です。
したがって、三角形ACPの面積は\(\frac{2}{3}\)なので、アの面積=三角形APRの面積=三角形ACPの面積×\(\frac{1}{3}\)=\(\frac{2}{3}\)×\(\frac{1}{3}\)=\(\frac{2}{9}\)です。

三角形ABCの面積を1にしたので、アの面積が\(\frac{2}{9}\)とわかった時点で、「アの面積は三角形ABCの面積の\(\frac{2}{9}\)倍」といえるのよ。
アの辺AP・辺ARは、三角形ABCの辺AB・辺ACの一部です。そして、アの面積は、三角形ABCの面積に\(\frac{AP}{AB}\)と\(\frac{AR}{AC}\)をかければ求められることもわかりました。つまり、アの面積=三角形ABCの面積×\(\frac{AP}{AB}\)×\(\frac{AR}{AC}\)=1×\(\frac{2}{3}\)×\(\frac{1}{3}\)です。
アと同じように考えると、
- イの面積=三角形ABCの面積×\(\frac{BP}{BA}\)×\(\frac{BQ}{BC}\)=1×\(\frac{1}{3}\)×\(\frac{1}{2}\)=\(\frac{1}{6}\)
- ウの面積=三角形ABCの面積=三角形ABCの面積×\(\frac{CQ}{CB}\)×\(\frac{CR}{CA}\)=1×\(\frac{BP}{AB}\)×\(\frac{2}{3}\)=\(\frac{1}{3}\)
また、エの面積=三角形ABCの面積-(アの面積+イの面積+ウの面積)=1-(\(\frac{2}{9}\)+\(\frac{1}{6}\)+\(\frac{1}{3}\))=\(\frac{5}{18}\)です。
以上より、△ABCの面積に対して、アの面積は\(\frac{2}{9}\)倍、イの面積は\(\frac{1}{6}\)倍、ウの面積は\(\frac{1}{3}\)倍、エの面積は\(\frac{5}{18}\)倍です。



コメント