「場合の数」の単元では、となり合う部分に同じ色をぬらないように色ぬりしていく問題がよく出ます。代表的なのが旗のぬり分け問題です。
「となり合う部分」を見つけよう
【例題】赤、青、黄、緑の4色があります。これらの色を使って、下の図のような旗のA,B,C,D,Eの5つの部分をぬり分けます。このとき、となり合う部分には同じ色をぬらないものとして、次の問に答えなさい。
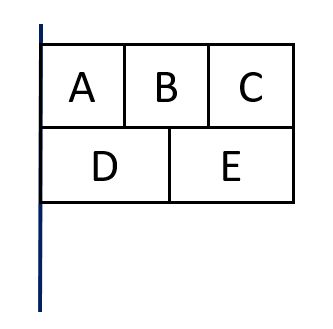
(1) 4色すべてを使ってぬり分ける方法は、全部で何通りありますか。
(2) 4色のうち何色使ってもよいとすると、ぬり分ける方法は全部で何通りありますか。
問題を考える前に、【例題】の「となり合う部分」について考えます。
「AとB」「BとC」「DとE」がとなり合う部分であるとわかるでしょう。しかし、となり合う部分はこの3組だけではありません。「AとD」「BとD」「BとE」「CとE」もとなり合う部分です。
「となり合う」という言葉から、横の関係だけを考えてはいけません。上下左右斜めのどこかで線(の一部)を一緒に使っている部分同士が「となり合う部分」です。
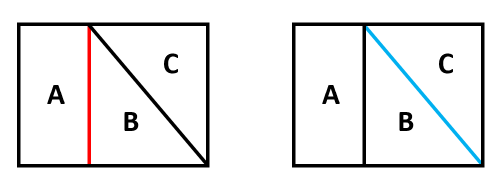
たとえば、下の図では、赤い線を一緒に使っているAとBがとなり合う部分です。青い線を一緒に使っているBとCもとなり合う部分です。一方、AとCは一緒に使っている線がないので、となり合う部分ではありません。
4色でぬり分けてみよう
(1)を解いてみましょう。
「4色で5つの部分をぬり分ける」とはどういうことかを考えます。
どの部分が同じ色になるか?
旗のぬり分け問題に限らず、場合の数では、とりあえず具体例を考えることが大切です。
(1)でも、絵を描いてみるとわかりやすくなります。
というわけで、2か所を赤でぬって、残りの部分を3色でぬるパターンをいくつか描いてみます。
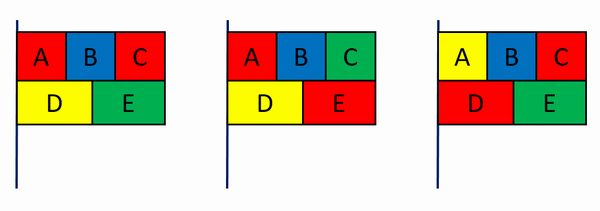
この絵からもわかる通り、赤でぬる2か所は「AとC」「AとE」「CとD」の3組です。これらの3組は、赤以外の色でぬることもできます。
色の選び方は何通りあるか?
次に、「AとC」を同じ色でぬるパターンを使って色の選び方を考えます。
「AとC」をぬる色は、4色から選べるので4通りです。
Bをぬる色は、「AとC」をぬった色を除いた3色から選べるので3通りです。
Dをぬる色は、A,B,Cをぬった色を除いた2色から選べるので2通りです。
Eをぬる色は、残っている1色なので1通りです。
それぞれの色の選び方はすべて同時に起こるので、積の法則から4×3×2×1=24(通り)です。
同じ色でぬる2か所は「AとC」か「AとE」か「CとD」のどれかなので、24通りが3パターンあると考えて、24×3=72(通り)が答です。
何色使ってもよい場合を考えよう
(2)では、4色すべてを使う場合以外に、そもそも何色使えるかを考える必要があります。やはり絵を描いてみるのが一番です。
何色使えばぬり分けられるか?
となり合う部分には同じ色をぬらないので、4色すべてを使う場合以外は、3色を使う1パターンしかありません。同じ色でぬるのは「AとE」と「CとD」です。
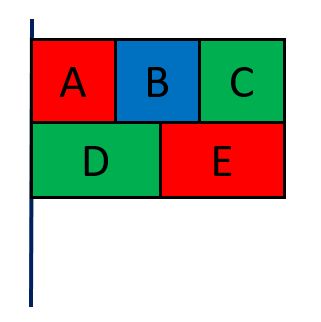
色の選び方は何通りあるか?
「AとE」をぬる色は、4色から選べるので4通りです。
「CとD」をぬる色は、「AとE」をぬった色を除いた3色から選べるので3通りです。
Bをぬる色は、A,C,D,Eをぬった色を除いた2色から選べるので2通りです。
それぞれの色の選び方はすべて同時に起こるので、積の法則から4×3×2×1=24(通り)です。
積の法則か?和の法則か?
最後に、4色すべてを使う場合((1)の答)と3色を使う場合の関係を考えます。
4色すべてを使う場合と3色を使う場合は同時に起こらないので、和の法則から72+24=96(通り)が答です。72×24(積の法則)ではないので要注意です。
絵を描いて考えよう
旗のぬり分け問題では、絵を描いてみると、どの部分を同じ色でぬるかがわかります。頭の中で考えてわからなくなるのではなく、手を動かしてみることが大切です。




コメント