問題演習コーナー
【問題】赤、青、黄、緑の4色を使って、下の図のような旗のA,B,C,Dの4つの部分をぬり分けます。4色のうち何色使ってもよいとすると、ぬり分ける方法は全部で何通りありますか。ただし、となり合う部分には同じ色をぬらないものとします。
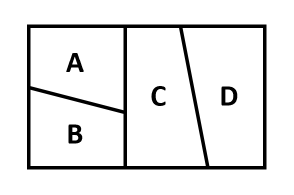
(ア)4色でぬり分ける場合
Aをぬる色は、4色から選べるので4通りです。
Bをぬる色は、Aをぬった色を除いた3色から選べるので3通りです。
Cをぬる色は、A,Bをぬった色を除いた2色から選べるので2通りです。
Dをぬる色は、残っている1色なので1通りです。
それぞれの色の選び方はすべて同時に起こるので、積の法則から4×3×2×1=24(通り)です。
(イ)3色でぬり分ける場合
下の図で、同じ色になる2か所を赤でぬってみました。「AとD」か「BとD」が同じ色になります。
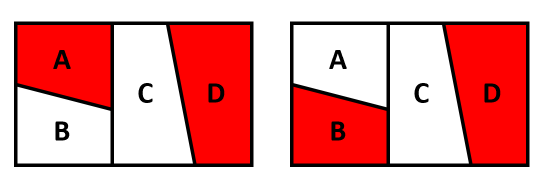
「AとD」を同じ色でぬるとします。
「AとD」をぬる色は、4色から選べるので4通りです。
Bをぬる色は、Aをぬった色を除いた3色から選べるので3通りです。
Cをぬる色は、A,Bをぬった色を除いた2色から選べるので2通りです。
それぞれの色の選び方はすべて同時に起こるので、積の法則から4×3×2=24(通り)です。
同じ色でぬる2か所は「AとD」か「BとD」のどちらかなので、24通りが2パターンあると考えて、24×2=48(通り)です。
(ア)と(イ)は同時に起こらないので、和の法則から24+48=72(通り)が答です。
トップ画像=Pixabay



コメント