問題演習コーナー
【問題】ある電車が150mの陸橋を渡り終わるまでに15秒かかり、240mのトンネルを通り抜けるまでに20秒かかりました。この電車の長さは何mですか。また、速さは時速何kmですか。
電車の長さを□m、速さを秒速△mとして、下の図を描きます。求める速さは時速ですが、陸橋やトンネルの長さが「m」で、かかる時間が「秒」で表されているので、「秒速△m」としました。
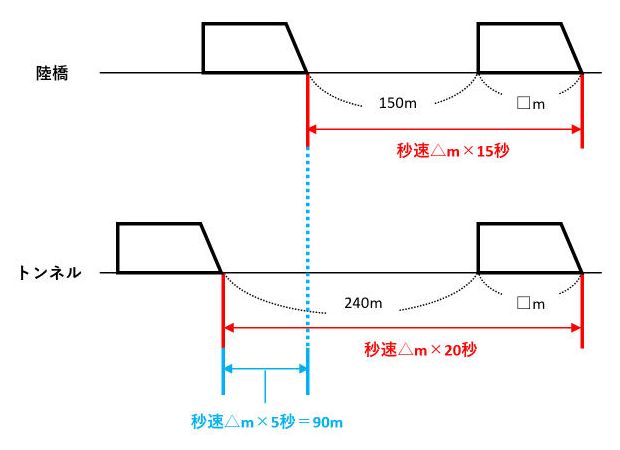
電車の先頭に注目して、電車が進んだ道のりを考えます。陸橋を渡り終わるまでの道のりとトンネルを通り抜けるまでの道のりの差（上の図の青い部分）は90m、時間の差は5秒なので、△＝90÷5＝18です。
電車の速さは、秒速18m＝18m÷1秒＝0.018km÷（1/3600）時間＝0.018×3600＝時速64.8kmです。速さの単位換算については、以下の記事を参考にして下さい。
【速さの単位換算法】時速を分速に変換するとき60で割るのは何故？
「時速→分速」「km→m」などの変換で「60で割るの？1000をかけるの？」と混乱しないためには、意味を理解して計算することが大切です。
mimizuku-edu.com
2016.01.16
電車の速さが秒速18mなので、秒速18m×15秒＝150m＋□mです。したがって、電車の長さは□＝18×15－150＝120（m）です。
別解（消去算として解いてみよう）
□と△を使って2つの式を作り、消去算として解くこともできます。
陸橋 △×15＝150＋□ … ①
トンネル △×20＝240＋□ … ②
②－①より、△×5＝90なので△＝18です。したがって、秒速18m＝時速64.8kmです。
△＝18を①に代入して、18×15＝150＋□なので□＝18×15－150＝120（m）です。
【消去算】連立方程式は小学生でも解ける！加減法と代入法は簡単だよ
いくつかわからない数があるとき、式を作ってこれらの数を求めるのが消去算です。中学数学の連立方程式を先取りし、加減法と代入法を理解しましょう。
mimizuku-edu.com
2021.10.04
① 電車が電柱の前を通過する問題と陸橋を渡る問題は、どこに違いがありますか。
（例）電柱は横の長さを考えませんが、陸橋は横の長さを考えます。
② 「電車が電柱の前を通過する」とはどういうことですか。
（例）電車の先頭が電柱に重なった後、同じ電車の最後尾が電柱に重なることです。
③ 通過算では何に注目しますか。
（例）電車の先頭か最後尾に注目します。
トップ画像＝写真AC
コメント