相似な三角形を円周角から導く！円に内接する長方形を題材とした難問

都立高校入試の令和3年度の過去問から、数学の大問4（平面図形）を解説します。

角の大きさを求める問題

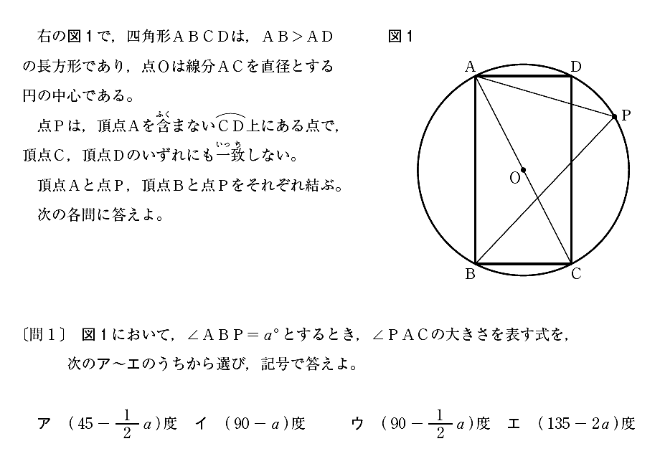
[問1]は∠PACの大きさを求める問題です。

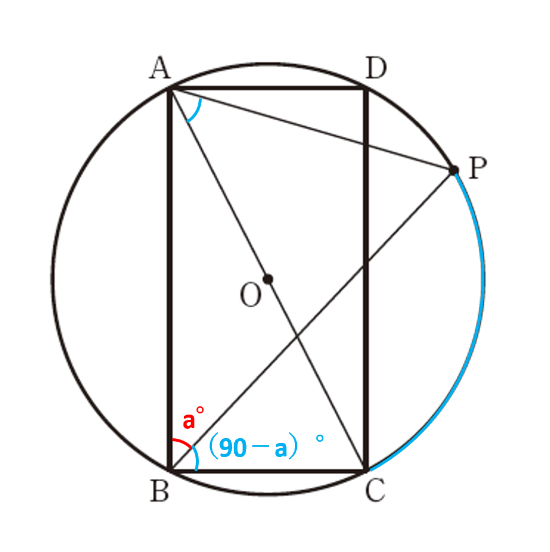
∠PBP＝a°、∠ABC＝90°なので、∠PBC＝90－a°です。∠PBCと∠PACはどちらも弧PCに対する円周角なので∠PBC＝∠PACです。したがって、∠PAC＝90－a°で、イが答えです。

円周角の定理で角度を簡単に求める！円に内接する図形の問題が面白い

円に内接する図形の角度を求める問題では円周角の定理を使います。この定理を利用して大きさの等しい円周角を見つける手順をわかりやすく解説します。

mimizuku-edu.com

2018.06.08

二等辺三角形であることを証明する問題

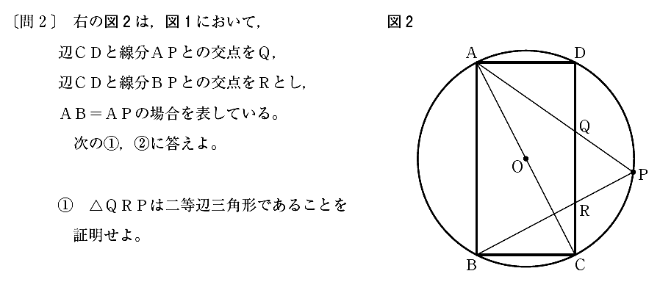
[問2]①は△QRPが二等辺三角形であることを証明する問題です。

仮定としてAB＝APなので、△ABPは二等辺三角形であるとわかります。ここから証明がスタートします。

模範解答は以下の通りです。

【別解】△QRP∽△ABPを証明する

模範解答とは違いますが、以下のように、△QRP∽△ABPを証明してもよいでしょう。

合同と相似を利用して面積を求める問題

[問2]②は△PRCの面積を求める問題です。

2点CとPを結んで△PRCを作り、△PRCと相似な三角形を探しますが、見つかりません。そこで△PRCを含む三角形を探します。

△BCPが△PRCを含みます。さらに、△APCが△PRCを含みます。

見た目からして△ABC≡△APCなので、△APC＝△ABC＝8×16×\(\frac{1}{2}\)＝64（cm²）といえそうです。ただ、見た目で合同と決めつけるわけにはいかないので証明しましょう。

△APCと△ABCにおいて、△APCは円の直径ACを一辺とするので∠APC＝90°で、∠APC＝∠ABC＝90°、ACは共通なので、直角三角形の斜辺と他の一辺がそれぞれ等しいから△APC≡△ABCです。

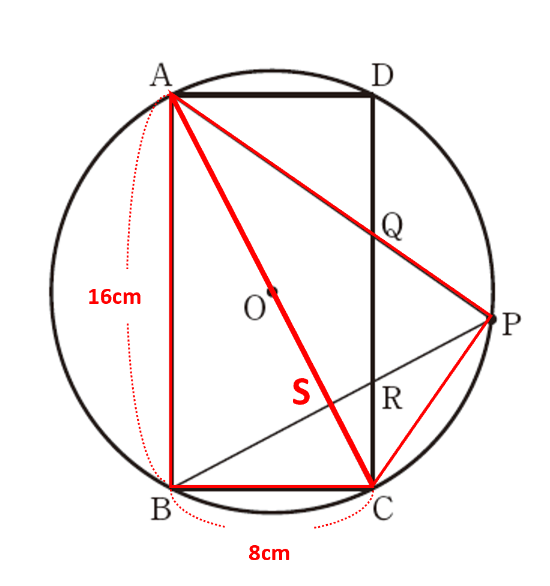
ACとBPの交点をSとすると、合同な三角形を2つくっつけた四角形の対角線で分割された三角形について、△ABS≡△APS、△BCS≡△PCSもわかります。

ここで△ABSと△PCSにおいて、対頂角より∠ASB＝∠PSC、弧BCに対する円周角より∠BAC＝∠CPB（∠BAS＝∠CPS）なので、2組の角がそれぞれ等しいから△ABC∽△PCSです。相似比はAB：PC＝16：8＝2：1より面積比は△ABS：△PCS＝4：1です。したがって、△BCP＝△PCS＋△BCS＝2△BCS＝2×\(\frac{1}{5}\)△ABC＝2×\(\frac{1}{5}\)×64＝\(\frac{128}{5}\)（cm²）を求められました。

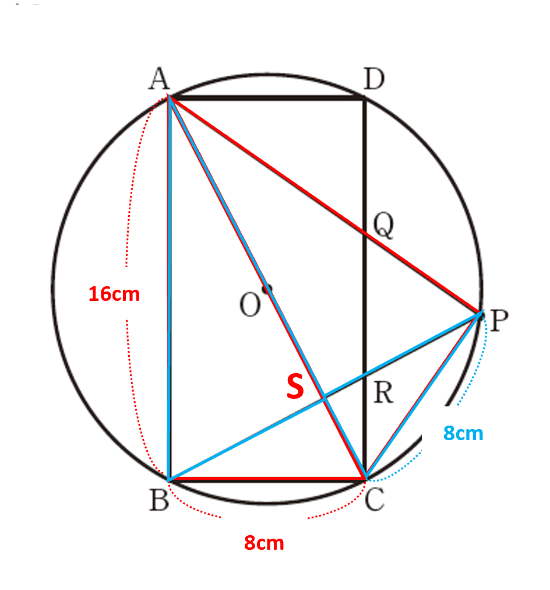
△BCPから△BCRを引けば△PRCなので、△BCRの面積を求めましょう。

△BCRと△ABCにおいて、△BCS≡△PCSかつ△ABC∽△PCSより∠CBR＝∠BAC、仮定より∠BCR＝∠ABCなので、2組の角がそれぞれ等しいから△BCR∽△ABCです。相似比はBC：AB＝8：12＝1：2より面積比は△BCR：△ABC＝1：4です。したがって、△BCR＝\(\frac{1}{4}\)△ABC＝\(\frac{1}{4}\)×64＝16（cm²）を求められました。

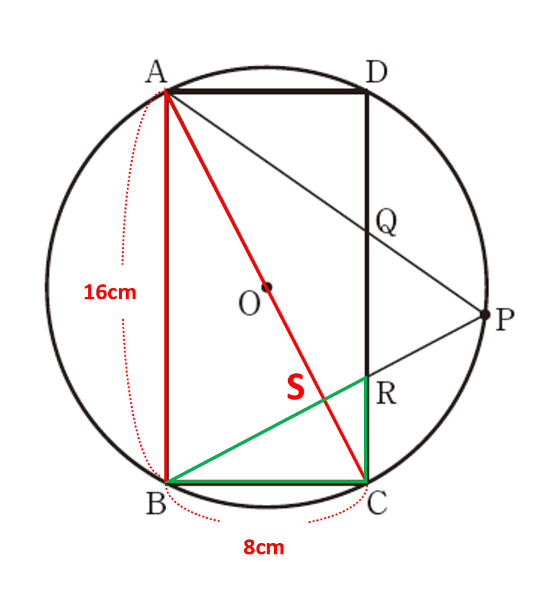
以上より、△PRC＝△BCP－△BCR＝\(\frac{128}{5}\)－16＝\(\underline{\frac{48}{5}}\)（cm²）が答えです。

特殊な図形であることの証明も練習しておこう

令和3年度の大問4は、円と円に内接する長方形に関する問題でした。

都教委が公表している正答率は、[問1]が64.8％、[問2]①が32.3％、[問2]②が0.5％です。

[問1]は、受験生の3人に2人は解ける簡単な問題です。

[問2]①の正答率が低いのは、単純な相似や合同の証明ではなく、二等辺三角形であることの証明に戸惑った受験生が多かったからだと考えられます。都立高校受験生は、特殊な図形であることの証明を普段から練習しておくとよいでしょう。

[問2]②は毎年難しいので、よほど数学が得意な受験生以外は捨て問扱いで構いません。もし解くのなら、相似や合同となる三角形をたくさん見つけていって、線分や面積の比をどんどん求めていく根気が必要です。

過去10年の都立高校入試問題を徹底分析して分野別にまとめた問題集「高校入試　虎の巻」で大問4の出題傾向を確認し、[問2]②まで解けるようにしておくとよいでしょう。

トップ画像＝Pixabay