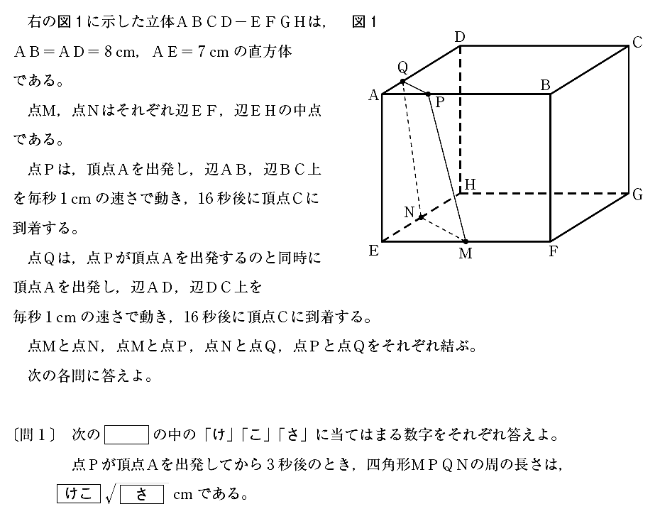
都立高校入試の令和4年度の過去問から、数学の大問5(空間図形)を解説します。
四角形の周の長さを求める問題
[問1]は四角形MPQNの周の長さを求める問題です。
△EMNと△APQはどちらも直角二等辺三角形です。したがって、1:1:\(\sqrt{2}\)の比を使って、MN=4\(\sqrt{2}\)cm、PQ=3\(\sqrt{2}\)cmです。
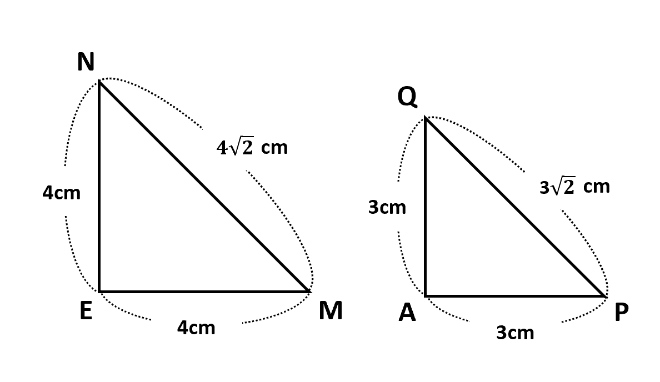
次に、四角形APMEに着目してPMの長さを求めます。PからEMに下ろした垂線とEMの交点をLとして、直角三角形PMLに三平方の定理を用います。PM=\(\sqrt{PL^2+ML^2}\)=\(\sqrt{7^2+1^2}\)=5\(\sqrt{2}\)(cm)です。また、QN=PM=5\(\sqrt{2}\)cmです。
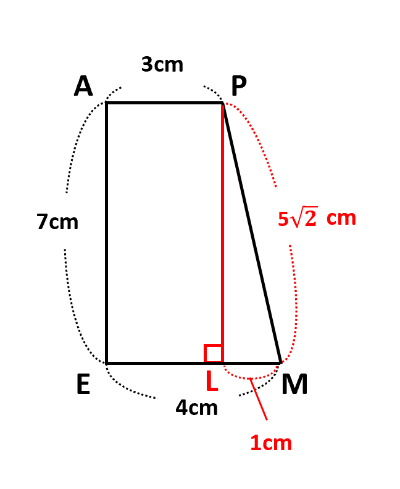
したがって、四角形MPQNの周の長さ=MN+PQ+PM+QN=4\(\sqrt{2}\)+3\(\sqrt{2}\)+5\(\sqrt{2}\)+5\(\sqrt{2}\)=\(\underline{17\sqrt{2}}\)(cm)です。
立体の体積を求める問題
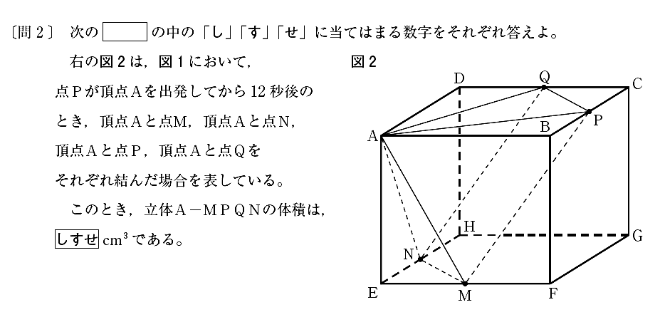
[問2]は立体A-MPQNの体積を求める問題です。
立体A-MPQNは面MPQNを底面とする四角錐です。面MPQNの面積を求め、頂点Aから面MPQNに下ろした垂線(高さ)の長さを求めましょう。
MNの中点をS、PQの中点をT、頂点Aから面MPQNに下ろした垂線と面MPQNの交点をUとします。
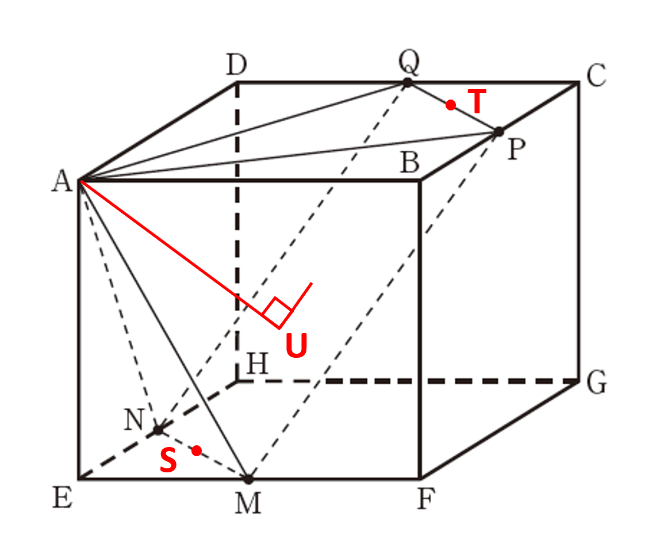
△EMNと△CPQはどちらも直角二等辺三角形です。さらに、点Pが頂点Aを出発してから12秒後なので、AB+BP=AD+DQ=12cmからBP=DQ=4cmで、△CPQ≡△EMNです。
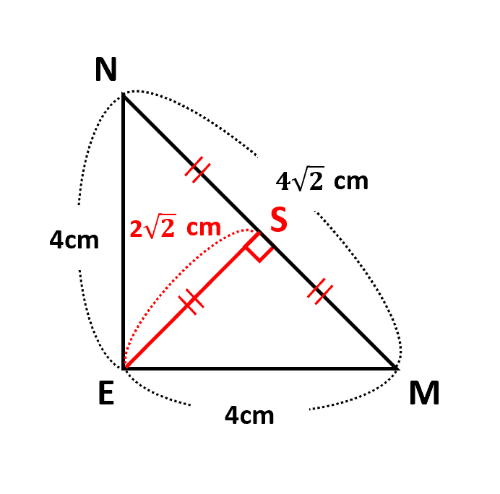
△EMNについて、下の図からES=2\(\sqrt{2}\)cmなので、CT=2\(\sqrt{2}\)cmもわかります。
面MPQNは長方形で、面ACGEと垂直です。さらに、UはST上にあり、3点U、S、Tはすべて面ACGE上にあります。面ACGEを描いたのが下の図です。
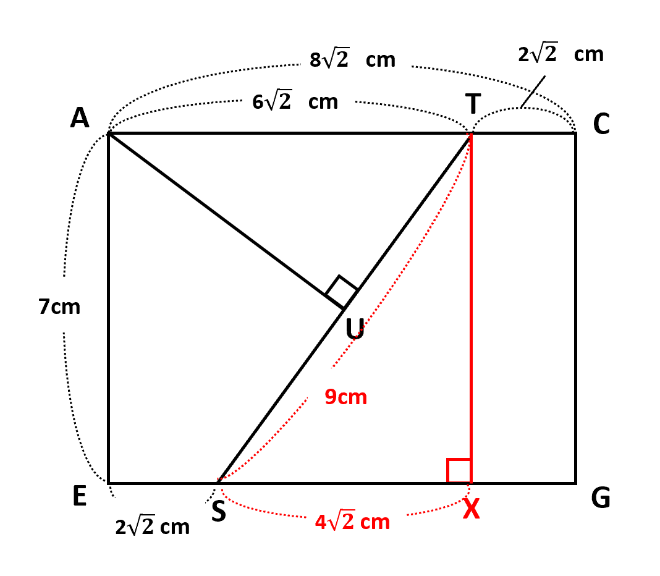
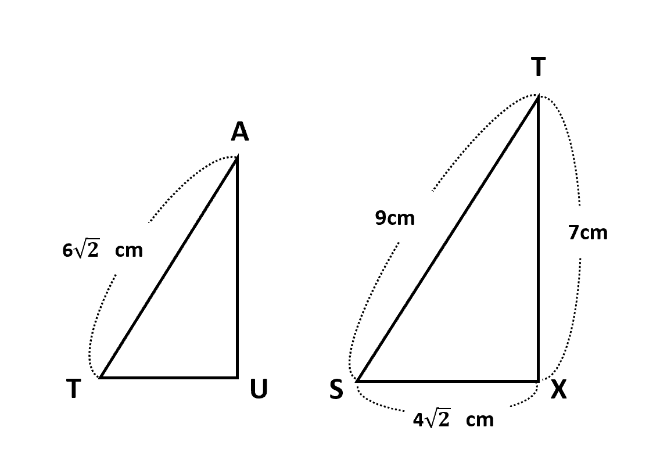
図には、TからEGに下ろした垂線とTとの交点Xを書き加えました。△TSXに三平方の定理を用いて、TS=\(\sqrt{SX^2+TX^2}\)=\(\sqrt{(4\sqrt{2})^2+7^2}\)=9(cm)です。
ここで△ATUと△TSXについて、∠AUT=∠TXS=90°、平行線の錯角は等しいので∠ATU=∠TSXより、2組の角がそれぞれ等しいので△ATU∽△TSXとわかります。△ATUと△TSXの相似比はAT:TS=6\(\sqrt{2}\):9=AU:TXなので、AU=\(\frac{6\sqrt{2}}{9}\)TX=\(\frac{6\sqrt{2}}{9}\)×7=\(\frac{14\sqrt{2}}{3}\)(cm)です。
また、面MPQNの面積=MN×TS=4\(\sqrt{2}\)×9=36\(\sqrt{2}\)(cm2)です。
したがって、立体A-MPQNの体積=面MPQN×AU×\(\frac{1}{3}\)=36\(\sqrt{2}\)×\(\frac{14\sqrt{2}}{3}\)×\(\frac{1}{3}\)=112(cm3)です。
直方体の中にできる図形を考えるのが難しい
令和4年度の大問5は、直方体の中にできる図形に関する問題でした。
都教委が公表している正答率は、[問1]が29.9%、[問2]が1.2%です。
[問1]は難しくありません。しかし、正答率が低かったことを考えると、そもそも「周の長さ」がわからない受験生や、勘違いしてしまった受験生が多かったのかもしれません。
[問2]は素直に底面積と高さを求めればよいだけですが、面ACGEで考える発想がないと手も足も出ないでしょう。最後の問題で時間的な余裕がなく、そもそも手を付けられなかった受験生も少なくなかったはずです。[問2]は毎年難しいので、よほど数学が得意な受験生以外は捨て問扱いで構いません。
過去10年の都立高校入試問題を徹底分析して分野別にまとめた問題集「高校入試 虎の巻」で大問4の出題傾向を確認し、[問1]だけでも解けるようにしておくとよいでしょう。
トップ画像=Pixabay



コメント