中学数学の関数分野に「グラフと図形」があります。xy平面上のグラフといくつかの点から図形を描き、それをもとにして未知の点の座標や関数の式を求める問題です。
「グラフと図形」は高校入試で頻出です。都立高校入試では、一般入試だけでなく、自校作成問題(グループ作成問題)でも、例年このタイプの問題が出題されます。
一方、多くの受験生は、「グラフと図形」を苦手とします。定期試験などであまり出題されず、対策が手薄になりがちだからです。
そんな「グラフと図形」の攻略法を紹介します。
「グラフと図形」の解法パターン
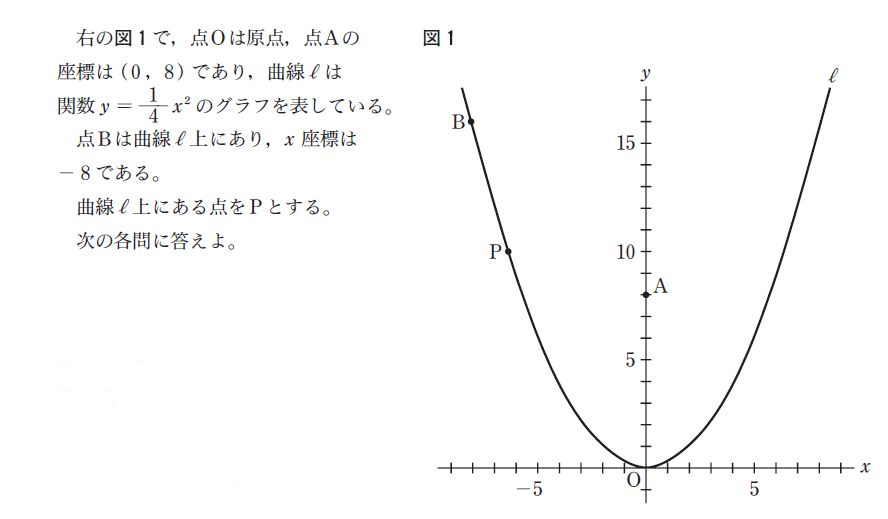
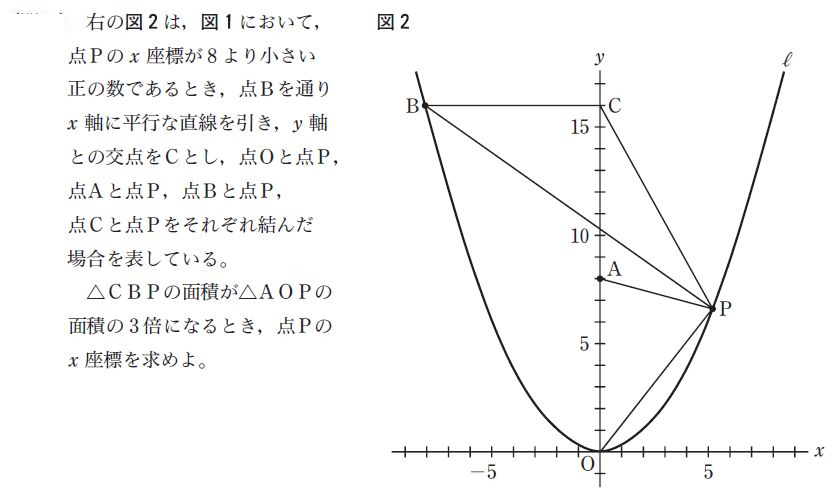
こちらの問題は、平成28年度の都立高校入試(一般入試)の大問3[問3]です。一見すると難しそうですね。
しかし、「グラフと図形」には解法パターンがあります。その解法に則って解けば、恐れるに足りません。
というわけで、「グラフと図形」の解法の手順を順に見ていきましょう。
未知の点のx座標を\(t\)とおく
まずは、未知の点のx座標を\(t\)とおきます。
今回の問題では、「点Pのx座標を求めよ」と指示されているので、Pのx座標を\(t\)とおきます。また、Pは二次関数のグラフ上にあるので、Pの座標は\(\left(t, \frac{1}{4}t^2\right)\)と表せます。
このように、\(t\)を使って、y座標や他の点の座標も表していきます。\(t\)以外の文字を使うとややこしくなるので、できる限り文字は\(t\)だけを使うようにしましょう。
\(t\)を使って問題文を式に変換する
次に、\(t\)を使って問題文を式に変換していきます。
たとえば、「△CBPの面積」と問題文にあるので、これを文字式で表します。
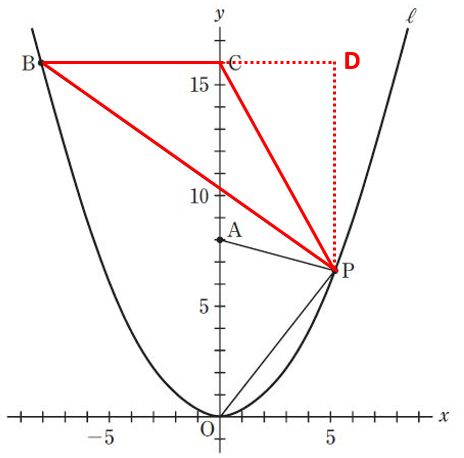
上図のように、BCの延長線にPから下ろした垂線の足(BCの延長線とPを通る垂線との交点)をDとします。
なぜこのようなことをしたかというと、中学数学の「グラフと図形」では、次の鉄則があるからです。
点と直線の距離を出す術を持たない中学生にとって、△CBPの底辺をBPやCPとすると、高さを求められなくなります。そのため、△CBPの底辺はBC、高さをDPとします。
ここで、BCとDPの長さを求めます。x軸右方向を正、y軸上方向を正とするxy平面上では、線分の長さを次の式で求めます。
- 横の線分の長さ…(右のx座標)-(左のx座標)
- 縦の線分の長さ…(上のy座標)-(下のy座標)
したがって、△CBPの面積は次の式になります。
同様に、「△AOPの面積」を次の式で表します(Eは、PからAOに下ろした垂線の足)。
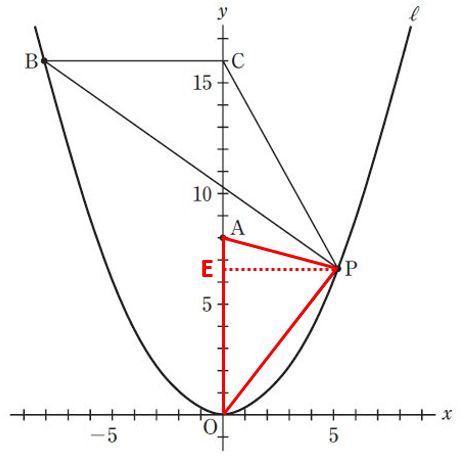
方程式を作って解く
最後に、方程式を作って解きます。
問題文には、「△CBPの面積は△AOPの面積の3倍」とあります。ここから、方程式を作って\(t\)の値を求めます。
△CBP=△AOP×3
64-\(t^2\)=4\(t\)×3
\(t^2\)+12\(t\)-64=0
(\(t\)+16)(\(t\)-4)=0
\(t\)=-16, 4
問題文に「Pのx座標が8より小さい正の数」とあるので、\(t\)=4を選んで、正解は4となります。
「グラフと図形」は全問正解を狙える!!
「グラフと図形」の問題は、解法がワンターンで、計算量も多くありません。他の図形問題(平面図形・空間図形)に比べると、大きく難易度が下がります。過去10年の都立高校入試問題を徹底分析して分野別にまとめた問題集「高校入試 虎の巻![]() 」を使って練習して、確実に正解してほしいところです。
」を使って練習して、確実に正解してほしいところです。
「未知の点のx座標を\(t\)とおいて、方程式を作って解く」という解法パターンは、高校数学でも活きてきます。中学生のうちに習得しておくことをお勧めします。苦手な受験生は、以下の問題集で練習するといいでしょう。
トップ画像=Pixabay
 |
数学 図形と関数・グラフの融合問題完全攻略272選 【入試頻出問題厳選】 (高校入試特訓シリーズ) 新品価格 |




コメント
関数と図形の問題は最も苦手で最初問題文を見ても全く持ってわかりませんでしたが解説がとてもわかりやすく私でも理解出来ました。
特に都立入試はこういう問題が出やすいので頑張りたいと思いますm(_ _)m
コメントありがとうございます。
お役に立ててよかったです。
関数と図形を苦手とする受験生は多いですが、慣れれば難しくない分野です。
類問をたくさん解いて、苦手意識を無くしてくださいませ。
応援しています!