都立高校入試の令和5年度の過去問から、数学の大問4(平面図形)を解説します。
角の大きさを求める問題
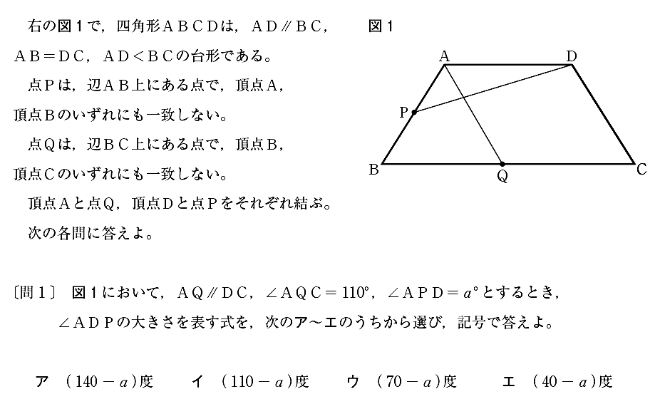
[問1]は∠ADPの大きさを求める問題です。
まずは、特殊な図形に着目して、角の大きさを求めていきます。
AD//BC、AQ//DCで、2組の対辺がそれぞれ平行なので、四角形AQCDは平行四辺形です。平行四辺形の対辺は等しいので、∠ADC=∠AQC=110°です。また、四角形ABCDはAB=ACの等脚台形なので、∠DAB=∠ADC=110°です。
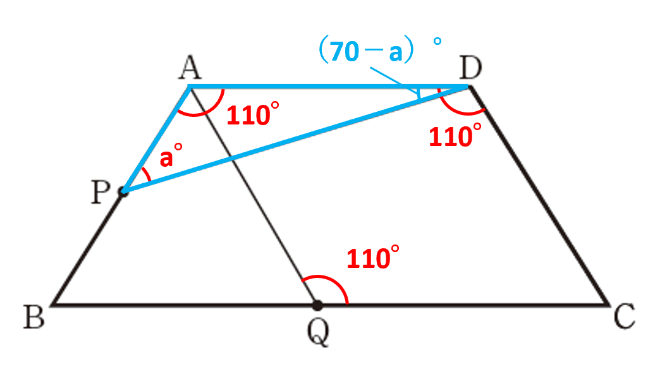
次に、△APDの内角の和は180°なので、∠ADP=180-∠APD-∠DAP(∠DAB)=180-a-110=70-a(°)となり、ウが答えです。
三角形の相似を証明する問題
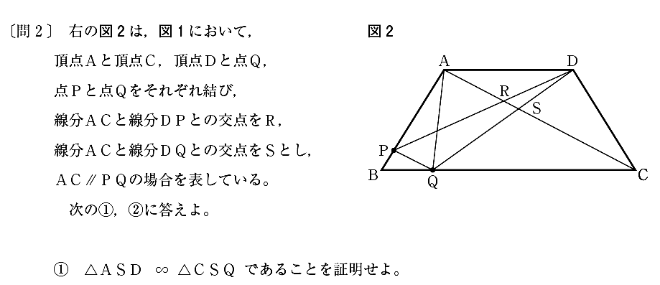
[問2]①は△ASDと△CSQが相似であることを証明する問題です。
AD//BCが仮定なので、平行線の錯角を使えばあっという間です。
△ASDと△CSQにおいて、
対頂角は等しいから、∠ASD=∠CSQ … (1)
AD//BCより、平行線の錯角は等しいから、∠ADS=∠CQS … (2)
(1)、(2)より、2組の角がそれぞれ等しいから、△ASD∽△CSQ
模範解答の(1)を、平行線の錯角の∠SAD=∠SCQにしても正解です。
相似比と底辺比を利用して面積比を求める問題
[問2]②は面積比を求める問題です。
AC//PQで平行線の同位角が等しいので、∠DRS=∠DPQ、∠DSR=∠DQPより、2組の角がそれぞれ等しいので△DRS∽△DPQです。[問2]①より△ASD∽△CSQで相似比はDS:QS=AD:CQ=2:3なので、DS:DQ=2:5です。したがって、RS:PQ=DS:DQ=2:5とわかりました。
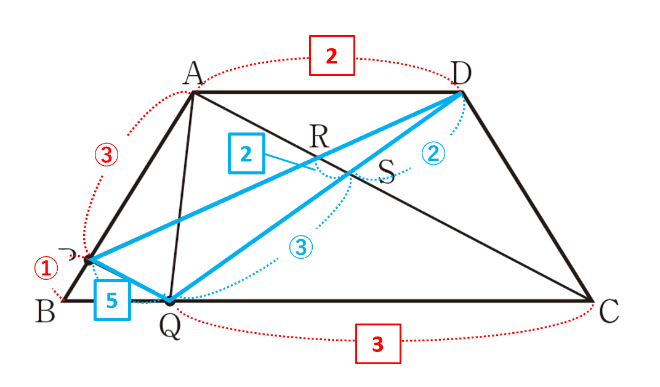
仮定よりAC//PQなので、平行線の同位角が等しいから∠BAC=∠BPQ、∠BCA=∠BQPとなり、2組の角がそれぞれ等しいので△BAC∽△BPQです。AP:PB=3:1より、BA:BP=BC:BQ=AC:PQ=4:1です。
RS:PQ=2:5とAC:PQ=4:1でPQの比をそろえてRS:PQ:AC=2:5:20なので、RS:AC=2:20=1:10とわかりました。
また、△ACDと△ABCは高さが等しいので、△ACDと△ABCの面積比は上底と下底の比に等しく、△ACD:△ABC=AD:BC=2:4=1:2です。したがって、△ACD=\(\frac{1}{3}\)台形ABCDとわかりました。
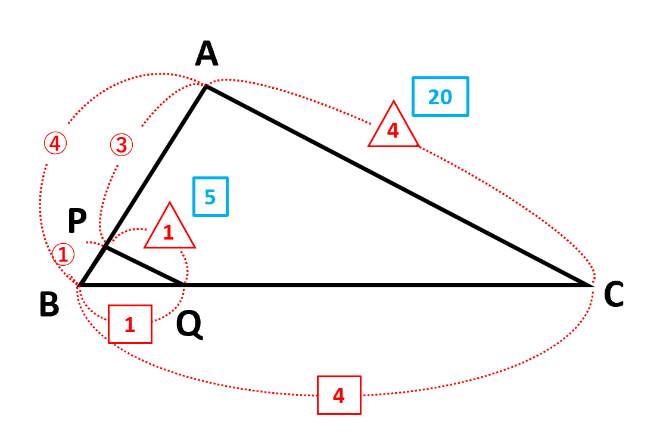
△DRSと△ACDは高さが等しいので、△DRS=\(\frac{1}{10}\)△ACD=\(\frac{1}{10}\)×\(\frac{1}{3}\)台形ABCD=\(\frac{1}{30}\)台形ABCDより、\(\underline{\frac{1}{30}}\)倍が答えです。
【別解】辺を延長する解き方
△DRSを含む△ASDを考えます。[問2]①より△ASD∽△CSQより、相似比はAS:CS=AD:CQ=2:3です。したがって、△ASD=\(\frac{2}{5}\)△ACDです。
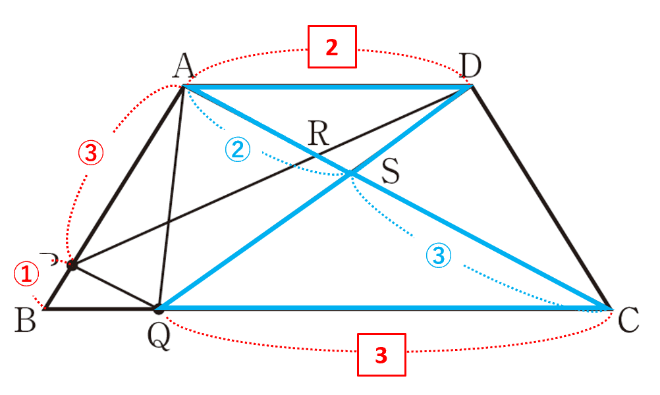
△ACDと△ABCは高さが等しいので、△ACDと△ABCの面積比は上底と下底の比に等しく、△ACD:△ABC=AD:BCです。
仮定よりAC//PQなので、平行線の同位角が等しいから∠BAC=∠BPQ、∠BCA=∠BQPとなり、2組の角がそれぞれ等しいので△BAC∽△BPQです。AP:PB=CQ:QB=3:1からBCの比=BQの比+QCの比=1+3=4となり、△ACD:△ABC=AD:BC=2:4=1:2です。したがって、△ACD=\(\frac{1}{3}\)台形ABCDなので、△ASD=\(\frac{2}{5}\)△ACD=\(\frac{2}{5}\)×\(\frac{1}{3}\)台形ABCD=\(\frac{2}{15}\)台形ABCDとわかりました。
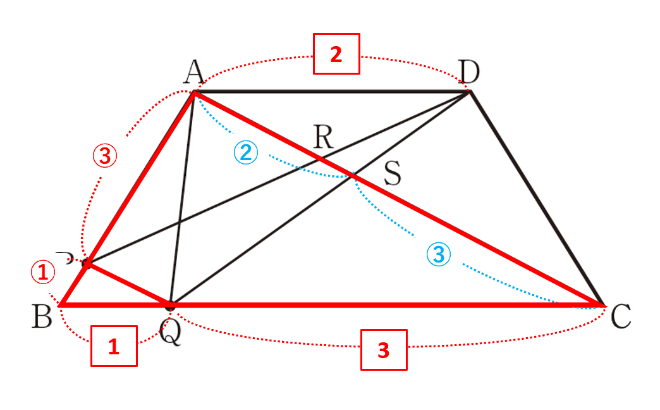
続いて、△DRSが△ASDの何倍かを求めるためAR:RSを考えます。
AR:RCを求めればよさそうですが、△ADRと相似な三角形がないので、RPとQBを延長してその交点をTとします。そうすると、△ADRと相似な△CTRができます。
△ADRと△CTRの相似比を求めるには、TBの比が必要です。そこでTBを含む△TBPに着目します。平行線の錯角が等しいから∠TBP=∠DAP、∠BTP=∠ADPとなり、2組の角がそれぞれ等しいので△TBP∽△DAPです。相似比はTB:DA=BP:AP=1:3より、DAの比が2ならばTBの比=\(\frac{1}{3}\)×2=\(\frac{2}{3}\)です。
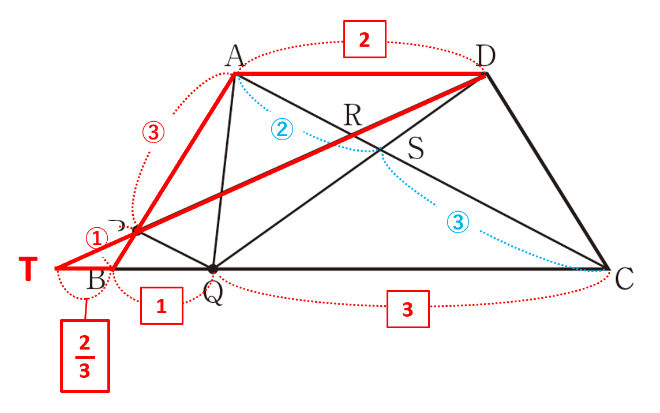
△ADRと△CTRの相似比はAD:CT=2:(\(\frac{2}{3}\)+4)=2:\(\frac{14}{3}\)=3:7=AR:CRとわかりました。
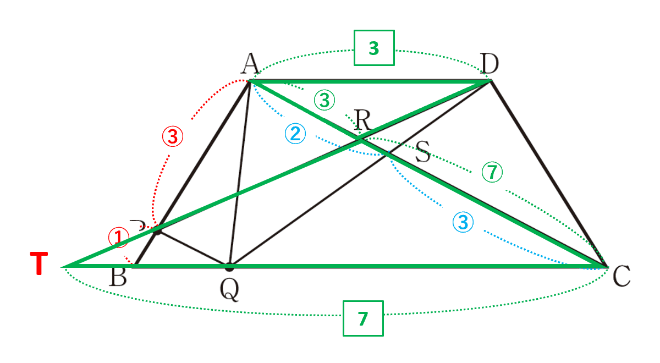
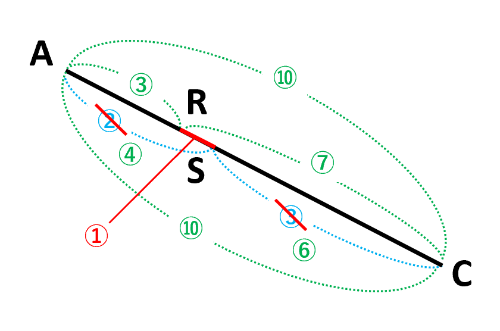
AR:CR=3:7とAS:CS=2:3について、全体の比を10にそろえるとAR:RS=3:1なので、△DRS=\(\frac{1}{4}\)△ASD=\(\frac{1}{4}\)×\(\frac{2}{15}\)台形ABCD=\(\frac{1}{30}\)台形ABCDより、\(\underline{\frac{1}{30}}\)倍が答えです。
証明問題は前年に比べて簡単になった
令和5年度の大問4は、[問2]①の証明問題が令和4年度に比べて非常に簡単でした。令和4年度の[問2]①は正答率が60%を下回ったため、さらに易しくしたのでしょう。

こうした難易度の調整があるため、都立高校受験生は、過去10年の都立高校入試問題を徹底分析して分野別にまとめた問題集「高校入試 虎の巻」で前年までの大問4を確認しておくとよいでしょう。
トップ画像=Pixabay

コメント