角の大きさを求める問題では、等しい大きさの角に注目することが大切です。
今回は、問題を解く上で役立つ角を3つ紹介します。
対頂角・同位角・錯角を覚えよう
等しい角としては、対頂角、平行線の同位角、平行線の錯角があります。どの角とどの角が同じ大きさになるのか、位置関係を覚えましょう。
対頂角
2本の直線が交わるとき、角アと角ウ、角イと角エのように向かい合う角を対頂角といいます。対頂角の大きさは等しいので、角ア=角ウ、角イ=角エです。
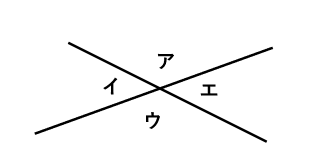

対頂角の大きさが等しいのはどうしてですか?

角ア+角イ=角イ+角ウ=180°だから、角イを引いた残りの角について角ア=角ウとなるんだよ。
3本以上の直線が1か所で交わる場合も、対頂角の大きさが等しくなります。たとえば、下の図では、角ア=角エ、角イ=角オ、角ウ=角カです。
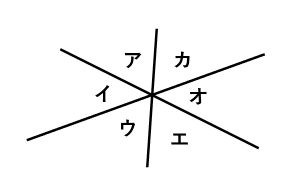

直線が増えると、どの角の大きさが等しいか、わからなくなります。

そういう場合は、角を作る直線に注目するといいよ。たとえば、下の図では、角アを作る直線は赤い直線と青い直線だ。この赤い直線と青い直線が作る角は、角アの他に角エだよね?このことから、角ア=角エがわかるんだ。
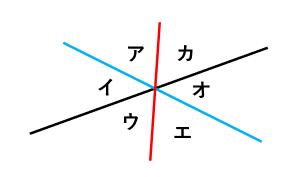
同位角と錯角
下の図のように、2本の直線に1本の直線が交わるとき、角アと角オ、角イと角カ、角ウと角キ、角エと角クは同位角です。同位角は同じ位置にある角です。
一方、角イと角ク、角ウと角オは錯角です。錯角はななめ向かいに位置する角です。
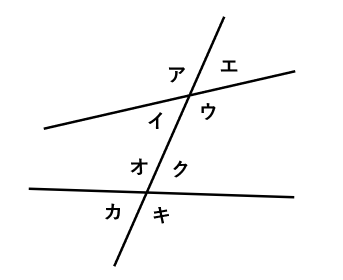
平行線の同位角と錯角
2本の直線をどこまで伸ばしても交わらないことを「平行」といいます。
下の図で、直線Aと直線Bが平行であるとき、同位角や錯角は等しくなります。
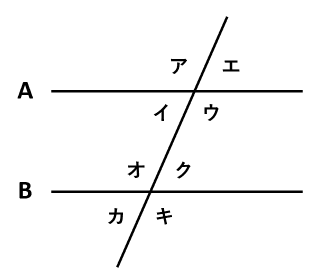
直線Aと直線Bが平行で同位角が等しいので、角ア=角オ、角イ=角カ、角ウ=角キ、角エ=角クです。
対頂角が等しいので、角ア=角ウ、角イ=角エ、角オ=角キ、角カ=角クです。
したがって、直線Aと直線Bが平行であるとき、角イ=角カ=角クより角イ=角ク、角ウ=角キ=角オより角ウ=角オが成り立つので、錯角が等しいこともわかります。

直線Aと直線Bが平行であるとき、同位角が等しいのはどうしてですか?

これを説明するのは難しいので、小学生のうちは結果だけ覚えておくといいよ。

直感的には、平行線の同位角の大きさが等しいとわかるんですが……

直感的にわかることほど、言葉で説明しようとすると難しいってことだね。
角度の問題を解いてみよう
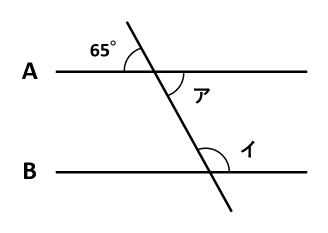
角アと65°は対頂角なので、角ア=65°です。
下の図で角ウ+65°=180°なので、角エ=180°-65°=115°です。角イと角ウは平行線の同位角なので、角イ=角ウ=115°です。
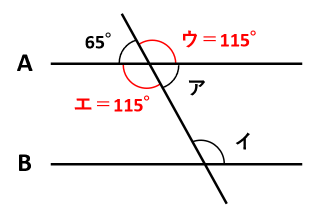
角エの大きさに注目しても解けます。
角エ+65°=180°なので、角エ=180°-65°=115°です。角イと角エは平行線の錯角なので、角イ=角エ=115°です。
平行線の錯角と同位角のどちらを使っても角イの大きさを求められます。
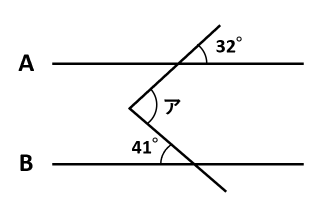
下の図のように、直線Aと直線Bに平行な直線Cを引いて、角ア=角イ+角ウにします。
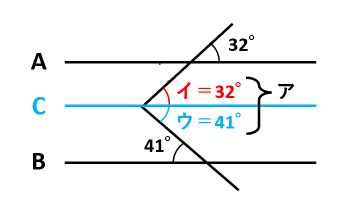
角イと32°は平行線の同位角なので、角イ=32°です。
角ウと41°は平行線の錯角なので、角ウ=41°です。
したがって、角ア=角イ+角ウ=32°+41°=73°です。

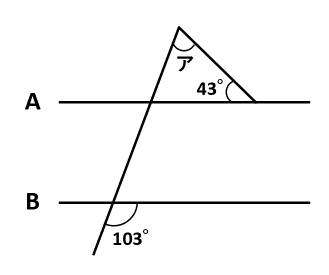
下の図で角イ+103°=180°なので、角イ=180°-103°=77°です。角イと角ウは平行線の同位角なので、角ウ=角イ=77°です。
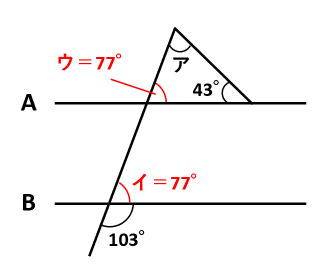
三角形の内角の和が180°であることを使います。角ア+角ウ+43°=180°なので、角ア=180°-角ウ-43°=180°-77°-43°=60°です。
補助線や三角形の内角の和を使おう
【例題2】では補助線を引きました。また、【例題3】では三角形の内角の和を使いました。
このように、平行線と角度の問題は、対頂角・同位角・錯角を知っているだけでは解けません。いろいろ工夫することが必要です。
多くの問題を解きながら、工夫のし方を身に付けていきましょう。
次の質問に答えましょう。(解答例は最後のページにあります)
① 対頂角、同位角、錯角はそれぞれどのような角ですか。
② 同位角や錯角が等しくなるのはどのような場合ですか。




コメント