【問題】太郎君は毎日、家から1500m離れた学校まで、一定の速さで25分間歩いて登校しています。ある日、家を出るのが5分遅くなったので、途中から歩きの速さの2倍の速さで走ったところ、いつもより1分早く学校に着きました。太郎君が走った道のりは何mですか。
速さの問題では、道のり・速さ・時間のうち2つの情報が与えられているなら、残り1つの足りない情報を求めてしまうのがポイントです。
「太郎君は毎日、家から1500m離れた学校まで、一定の速さで25分間歩いて登校しています」では、道のり1500mと時間25分間が与えられています。したがって、残り一つの足りない情報は太郎君の歩きの速さだとわかります。
歩きの速さは1500÷25=(分速)60(m)です。「歩きの速さの2倍の速さで走った」とあるので、歩きの速さを2倍した分速120mが走りの速さです。
また、「家を出るのが5分遅くなった」「いつもより1分早く学校に着きました」から、ある日の太郎君の移動時間は25-5-1=19(分)です。
移動の途中で速さを変える問題で、速さと移動時間の合計が分かっている場合、面積図を描いてみましょう。そうすると、つるかめ算と同じ方法で解けることに気づくでしょう。
つるかめ算については、以下の記事を参考にしてください。

この問題で面積図を描いて、つるかめ算と同じように考えると次の通りです。
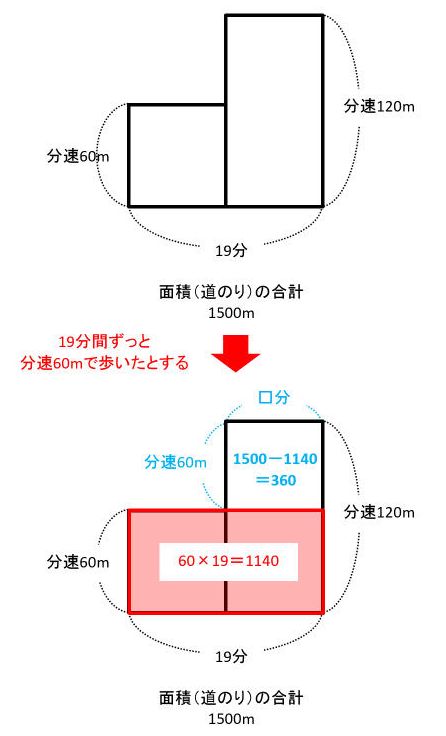
下の図から、□=360÷60=6(分)で、これが走った時間です。したがって、走った道のりは120×6=720(m)です。

速さの問題でもつるかめ算を使うんだね!
① 「時速」とは何ですか。
(例)1時間で進む道のりです。
② 速さが一定(同じ)のとき、道のりと時間はどのような関係になっていますか。
(例)道のりと時間は比例関係です。
③ 道のり・速さ・時間の関係を面積図で表すとき、それぞれは長方形のどこに対応しますか。
(例)長方形の縦が速さに、横が時間に、面積が道のりに対応します。
④ ダイヤグラムでは、速さはどのように表されますか。
(例)直線の傾きで表されます。
⑤ ダイヤグラムでは、どのような図形を見つけるといいですか。
(例)道のり・速さ・時間のうち2つの情報の分かっている直角三角形を見つけます。
トップ画像=写真AC



コメント