算数の基礎となる足し算・引き算・かけ算・わり算を四則計算といいます。今回は、整数の四則計算を図で表す方法と基本的な逆算（□を求める計算）を紹介します。
足し算・引き算は線分図で表そう
足し算は加法ともいい、その答は和です。引き算は減法ともいい、その答は差です。
足し算と引き算は、次のような線分図で表せます。
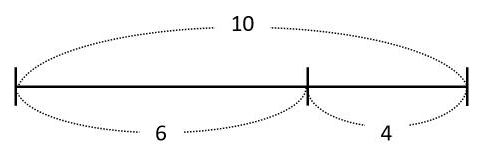
この線分図から、6＋4＝10という足し算の式を作れます。また、6と4を入れかえて、4＋6＝10も成り立つことがわかります。
一方、引き算の式は、10－6＝4と10－4＝6の2種類を作れます。10－6＝4で10と6を入れかえることはできません。
線分図で考えれば、足し算・引き算の逆算がどうして成り立つのかも理解できるでしょう。
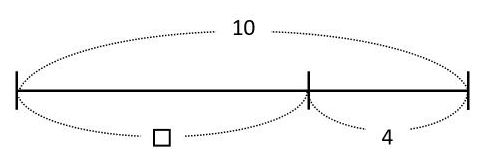
足し算の逆算は次の通りです。
□＋4＝10 → □＝10－4
4＋□＝10 → □＝10－4
引き算の逆算は次の通りです。
このタイプの引き算では、－の後ろの□と＝の後ろの数を入れかえられます。
また、次の線分図は、別のタイプの引き算の逆算を表しています。
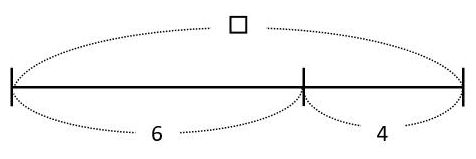
□－6＝4 → □＝4＋6
□－4＝6 → □＝6＋4
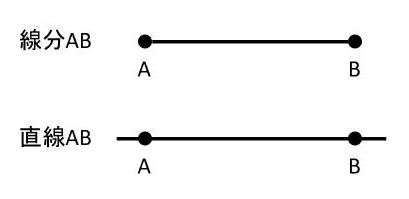
「線分」と「直線」って違うんですか？
下の図のように、点Aと点Bで止まっている直線を「線分AB」というんだ。これに対して、「直線AB」といったら、点Aと点Bを通り過ぎてずっと伸びていくよ。
かけ算・わり算は面積図で表そう
かけ算は乗法ともいい、その答は積です。わり算は除法ともいい、その答は商です。
かけ算とわり算は、次のような面積図で表せます。面積図では、「たて×横」の式で表される長方形の面積を使います。
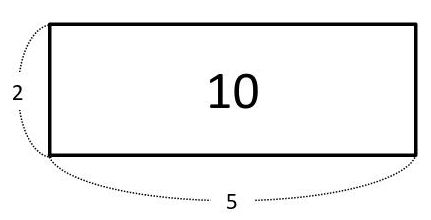
「たて×横＝面積」なので、2×5＝10というかけ算の式を作れます。また、「面積÷たて＝横」から10÷2＝5、「面積÷横＝たて」から10÷5＝2というわり算の式をそれぞれ作れます。10÷2＝5で10と2を入れかえることはできません。
次の面積図から、かけ算・わり算の逆算を理解しましょう。
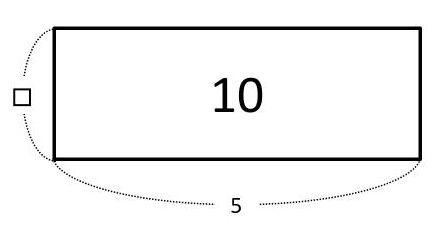
かけ算の逆算は次の通りです。
□×5＝10 → □＝10÷5
5×□＝10 → □＝10÷5（×の前後は入れかえられます）
わり算の逆算は次の通りです。
このタイプのわり算では、÷の後ろの□と＝の後ろの数を入れかえられます。
また、次の線分図は、別のタイプのわり算の逆算を表しています。
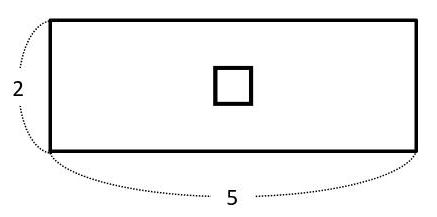
□÷2＝5 → □＝5×2
□÷5＝2 → □＝2×5
方程式の考え方から逆算の式を理解しよう
＝（イコール）は、答を出すための記号ではなく、「同じ」という意味の記号です。そのため、＝で結ばれているものはすべて等しくなければなりません。
たとえば、2＋4＝6は正しいです。一方、2＋4＝6÷2＝3は、2＋4の計算結果である6と最後の3が等しいという意味になってしまうので正しくありません。中学受験算数では、この＝の使い方がとても大切です。
さて、□＋4＝10のように、わからない数（□など）を含み、最初から＝がある式（等式）を方程式といいます。
方程式に含まれる□などは、ある数では＝が成り立ちますが、それ以外の数では＝が成り立ちません。□＋4＝10は、□＝6のとき6＋4＝10ですが、□＝5のときは5＋4＝9≠10です。
方程式の＝の左側を「左辺（さへん）」、右側を「右辺（うへん）」、左辺と右辺を合わせて「両辺（りょうへん）」といいます。□＋4＝10は、□＋4が左辺、10が右辺、□＋4と10を合わせて両辺です。
方程式では、両辺に同じことをしても＝の関係はくずれません。□＋4＝10の両辺から4を引いても＝のままだということです。
□＋4＝10
□＋4－4＝10－4
左辺の4－4＝0なので、
□＝10－4
両辺に同じことをした結果、前ページの逆算の式になりました。
ここでは両辺に同じ数を足しましたが、同じ数を引くこともできます。同じ数をかけたり、同じ数でわったりしてもOKです。
「両辺に同じことをしても＝の関係がくずれない」に納得できない場合、次のように考えてみてください。
6＋4＝10
6＋4－4＝10－4
6＝10－4
□がない数字だけの等式だと、「両辺に同じことをしても＝の関係がくずれない」が正しいことがよくわかります。
「中学入試では、方程式を使ってはいけない」という話を聞きますが、本当ですか？
受験する中学が「方程式禁止」と明言していない限り、使っていけないことはないだろう。そもそも、答だけ書かせる問題なら、受験生がどんな方法で解いても、採点者にはわからないしね。ただ、きちんと方程式を使いこなすには、中学数学の正負の数や文字式の知識が必要になる。そうした知識のない小学生は、方程式の考え方に軽く触れる程度にしておいた方がいいと思うよ。
逆算をすらすらできるようにしよう
四則計算の逆算が成り立つ理由は、線分図・面積図や方程式から明らかです。このように「なぜ成り立つのか？」を考えることは、応用力をきたえる上で大切です。
一方で、逆算は、いちいち図などを使わなくても、パッと計算できなければなりません。次の式変形はしっかり頭に入れておきましょう。
【足し算】 □＋A＝B → □＝B－A A＋□＝B → □＝B－A
【引き算】 □－A＝B → □＝B＋A A－□＝B → □＝A－B
【かけ算】 □×A＝B → □＝B÷A A×□＝B → □＝B÷A
【わり算】 □÷A＝B → □＝B×A A÷□＝B → □＝A÷B
引き算とわり算の式変形の中でも、線を引いた逆算は特に役立ちます。ただし、AとBの位置をまちがえないように注意が必要です。
逆算をすらすらできることが、中学受験算数を得意にするための第一歩です。
次の質問に答えましょう。（解答例は最後のページにあります）
① 四則計算はどのような図で表せますか。
② ＝（イコール）はどのような意味の記号ですか。
③ 方程式の両辺に同じ数をかけました。どうなりますか。
コメント