ダイヤグラム(進行グラフ)を描きながら、速さと比の関係を図形的に考えましょう。
道のり・速さ・時間の中で一定のものはどれ?
速さは、単位時間(1時間・1分間・1秒間)あたりに進む道のりです。「道のり=速さ×時間」「速さ=道のり÷時間」「時間=道のり÷速さ」の3つの式は誰でも知っています。
さらに速さの応用として次の3つの考え方が登場します。
- 道のりが一定(同じ)ならば、速さの比と時間の比は逆比。
- 速さが一定(同じ)ならば、道のりの比は時間の比に等しい。
- 時間が一定(同じ)ならば、道のりの比は速さの比に等しい。

3つの考え方でいつも混乱します。どうやったらきちんと覚えられますか?

覚えるというよりも、ちょっと考えればわかることだよ。たとえば、速さがずっと同じならば、時間が経てば経つほど、進む道のりも長くなっていく。このことから「速さが一定ならば、道のりの比は時間の比に等しい」といえるよね?

2人が同じ場所からスタートしてゴールを目指すとき、足の速い人は遅い人より早くゴールに到着します。これが「道のりが一定ならば、速さの比と時間の比は逆比」ってことですね!

その通り!速さと比の問題では「道のり・速さ・時間の中で一定のものはどれ?」を常に意識することが大切だよ。
速さと比をダイヤグラムで図形的に表す
速さと比をダイヤグラム(進行グラフ)で図形的に表してみましょう。
速さが一定(同じ)の場合
速さが一定(同じ)の場合のシンプルな例が下の図です。
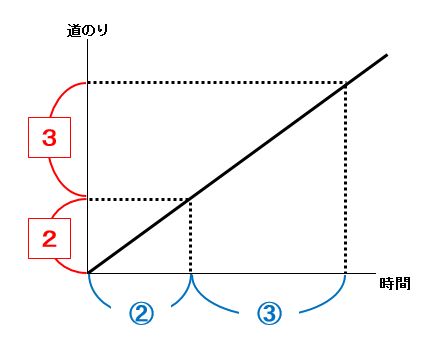
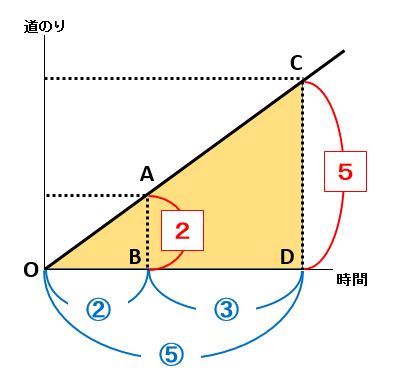
一定の速さで歩く人について、歩いた時間の比が2:3ならば、進んだ道のりの比も2:3です。平行線と比の関係から、相似な2つの三角形と考えることもできます(下の図で△OABと△OCDは相似)。

先生、算数のテキストに「往復の旅人算(出会い算)では、2人が2度目に出会うまでの時間は、はじめて出会うまでの時間の3倍です」と書かれているんですが、これも速さが一定の場合なんですか?

そうだよ。2人の速さの和が一定だから、道のりの比と時間の比が等しくなるんだ。下の図を見ると、2人が進んだ道のりの合計が、黄色の部分:紫の部分=片道分:往復分=1:2になっている。
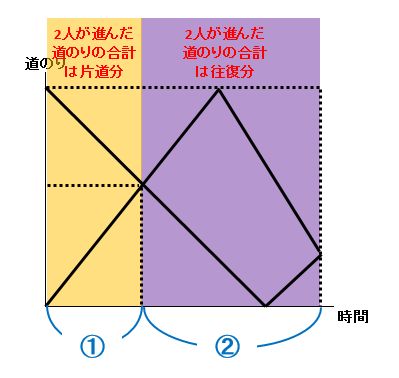

2人が進み始めてからはじめて出会うまでの時間を①とすると、はじめて出会ってから2度目に出会うまでの時間は②ですね。だから、①+②=③で3倍なんですね!
時間が一定(同じ)の場合
時間が一定(同じ)の場合のシンプルな例が下の図です。
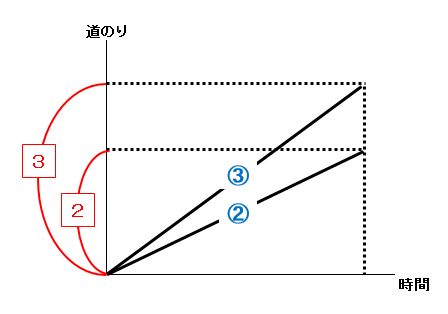
速さの比が2:3の2人が同じ時間歩くと、進んだ道のりも2:3になります。
この考え方を使うと解きやすいのが、旅人算の中の出会い算です。2人の速さの比が、出会った地点の道のりを求めるのに役立ちます(下の図参照)。
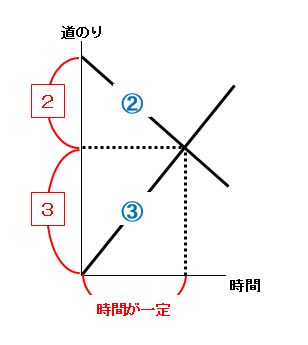
ポイントは、時間が一定の三角形を見つけることです。
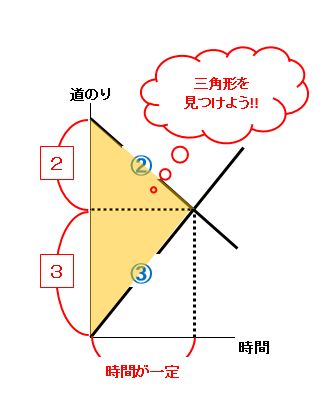
道のりが一定(同じ)の場合
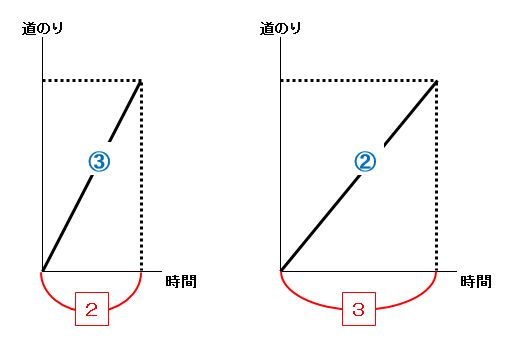
道のりが一定(同じ)の場合のシンプルな例は下の図ですが、これだけでは何がどう便利なのかわかりません。ダイヤグラムと逆比を使って解く旅人算をこの後で解説します。
旅人算をダイヤグラムと逆比を使って解く
ダイヤグラムと逆比を使って旅人算を解いてみましょう。出会い算でも追い越し算でも、道のりが一定になる三角形を見つけるのがコツです。
出会い算をダイヤグラムと逆比を使って解く
出会い算のダイヤグラムで、道のりが一定になる三角形を見つましょう。たとえば、速さの比がわかっている場合、下の図のように時間の比もわかります。
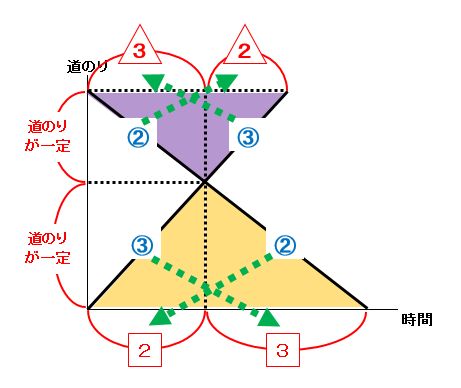
【例題1】兄はA地を弟はB地を同時に出発して向かい合って進んだところ、兄は出発してから12分後に弟と出会い、その9分後にB地に着きました。
(1) 兄と弟の速さの比を求めなさい。
(2) 弟はB地を出発してから何分後にA地に着きますか。
道のりが一定になる三角形を見つけて、比をどんどん書き込んでいきます。
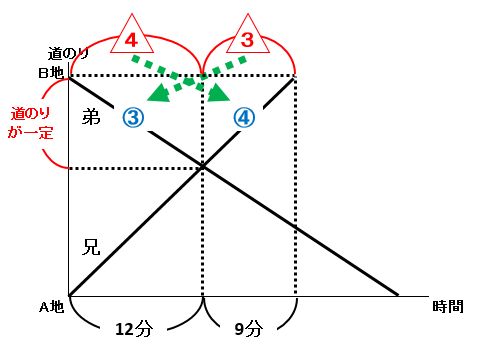
(1)は、上の図より、兄の時間:弟の時間=9分:12分=3:4なので、逆比にして兄の速さ:弟の速さ=4:3です。
続いて、(1)の結果を使って(2)も解きましょう。
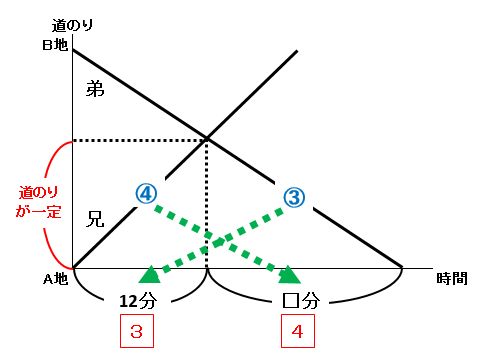
上の図より、兄の速さ:弟の速さ=4:3を逆比にして、兄の時間:弟の時間=3:4=12分:□分です。したがって、□=12÷3×4=16(分)なので、答は12+16=28(分後)です。
追い越し算をダイヤグラムと逆比を使って解く
追い越し算のダイヤグラムでも、道のりが一定になる三角形を見つましょう。たとえば、速さの比がわかっている場合、下の図のように時間の比もわかります。
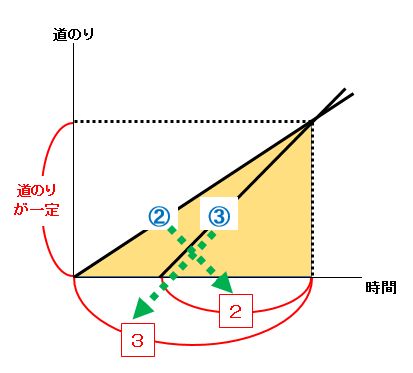
時間の比の位置をまちがわないように注意しましょう。
道のりが一定になる三角形を見つけて比をどんどん書き込めば、すぐに答を求められます。
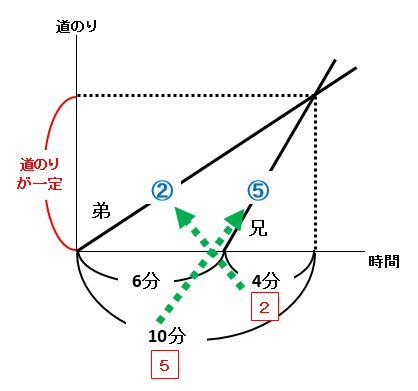
上の図より、兄の時間:弟の時間=4分:10分=2:5を逆比にして、兄の速さ:弟の速さ=5:2です。
ダイヤグラムと比は応用問題で役に立つ
基本的な出会い算や追い越し算だけだと、わざわざダイヤグラムを描いたり、比を使ったりするメリットを実感できないかもしれません。しかし、ダイヤグラムと比は応用問題で必ず役に立つので、しっかり練習しておくとよいでしょう。
トップ画像=写真AC




コメント