【過不足算】面積図を描ければ余りや不足を足すか引くかで悩まない！

あまりと不足の問題以外にも、さまざまな問題を考えてみましょう。

ちょうどと余りの問題

【例題2】何人かの子どもにあめ玉を配ります。1人7個ずつ配るとちょうど配ることができ、1人5個ずつ配ると20個余ります。子どもは何人いますか。

7個ずつ配った場合、あまりも不足もありません。このとき、配ろうとしたあめ玉の個数は実際のあめ玉の個数と同じです（左側の長方形）。

一方、5個ずつ配った場合、20個あまります。このとき、配ろうとしたあめ玉の個数は実際のあめ玉の個数より少ないので、右の長方形は左の長方形より小さくなります。

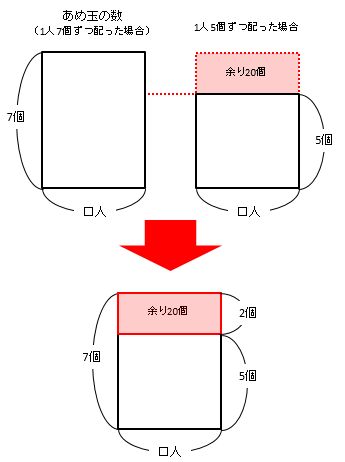
20個の長方形を見て、2×□＝20から□＝20÷2＝10人が答です。

エノキさん

あめ玉の個数は7×10＝70個よ。

【例題3】何人かの子どもにあめ玉を配ります。1人10個ずつ配ると20個不足し、1人6個ずつ配っても4個不足します。あめ玉は何個ありますか。

10個ずつ配った場合、20個不足します。このとき、配ろうとしたあめ玉の個数は実際のあめ玉の個数より多いので、左の長方形は右の長方形より大きくなります。

同じように、6個ずつ配った場合、4個不足します。このとき、配ろうとしたあめ玉の個数は実際のあめ玉の個数より多いので、真ん中の長方形は右の長方形より小さくなります。

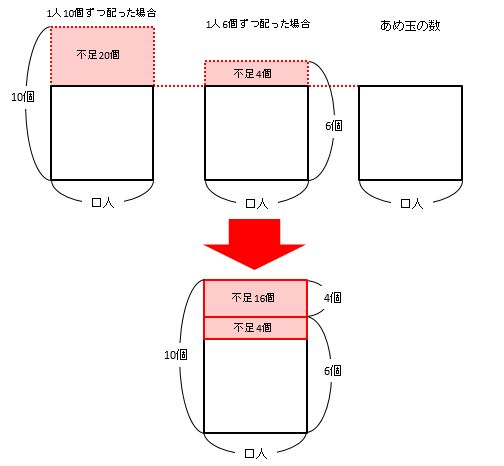
20ー4＝16個の長方形を見て、4×□＝16から□＝16÷4＝4人が子どもの人数です。しかし、【例題3】で求めなければならないのがあめ玉の個数なので、ここで終わりではありません。

あめ玉の個数は10×4ー20か6×4ー4を計算して20個が答です。

過不足算で「あまりと不足は足す、あまりとあまりは引く、不足と不足は引く」を公式のように覚えるのも悪くありませんが、忘れてしまったときに困ってしまいます。

しかし、面積図（や線分図）を描ければ、そもそもあまりや不足を足すか引くかで悩む必要は無くなります。

頭の中でパパッと計算しようとせず、図を描きながら考えることが大切です。

トップ画像＝写真AC