「時間と時刻」は小学1~3年の内容です。さらに小学6年では、分数のかけ算や割り算を学んだ後、時間を分数で表す方法も学びます。
算数で何度も出てくる「時間と時刻」ですが、最後の最後までよくわからないままの小学生が少なくありません。「時間の計算が出たら諦めよう」と思っている中学受験生もいるでしょう。
今回は、さまざまな時間の計算をわかりやすく解説します。
時刻を計算で求めよう
まずは、【例題1】の数字の意味を確認しましょう。
「10月15日午後1時24分」は時刻ですが、「2日15時間46分」は時間です。時刻と時間は次のように区別します。
- 時刻…ある瞬間のこと。
- 時間…時刻と時刻の間の長さ。
「7時30分に家を出る」の「7時30分」は時刻ですが、「7時間30分後に到着する」の「7時間30分」は時間です。「●時」は時刻で「●時間」は時間を表しますが、「■日」や「▲分」は時刻か時間か見た目でわからないので要注意です。
【例題1】のように、時刻に時間を足したり、時刻から時間を引いたりすると時刻を求められます。時刻同士を引いた結果は時間です。また、時間同士は、足し算や引き算だけでなく、かけ算や割り算、比の計算になっていることもあります。
時間(時刻)の計算は、普通の数字と同じように計算できるとは限りません。なぜなら24時制と60進法で考えなければならないからです。
1日を24時間とする24時制
単位を「時間」だけで考えるなら、17時間+14時間=31時間です。しかし、「日」も使うと、1日は24時間なので、31時間=24時間+7時間=1日7時間です。
このように、1日を24時間とする時間の考え方を「24時制」といいます。
24時制では、「午前3時」「午後5時」のように「午前」「午後」を使いません。「午前3時」ならば「3時」、「午後5時」ならば「17時」です。「午前□時」は「□時」、「午後△時」は「△+12時」で表します。
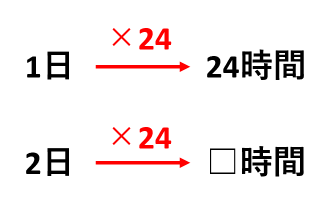
1日が24時間なので、「日」を「時間」に変換するときは、24をかければよいことがわかります。
- 2日は2×24=48時間
- 0.5日は0.5×24=12時間
- \(\frac{5}{3}\)日は\(\frac{5}{3}\)×24=40時間
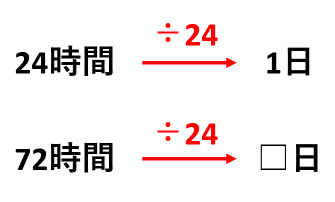
逆に、「時間」を「日」に変換するときは、24で割ります。
- 72時間は72÷24=3日
- 2.4時間は2.4÷24=0.1日
- 36時間は36÷24=\(\frac{3}{2}\)日(1.5日)
1時間を60分とする60進法
単位を「分」だけで考えるなら、35分+47分=82分です。しかし、「時間」も使うと、1時間は60分なので、82分=60分+22分=1時間22分です。
60分を1時間、60秒を1分とするように、60で繰り上がる数の表し方を「60進法」といいます。
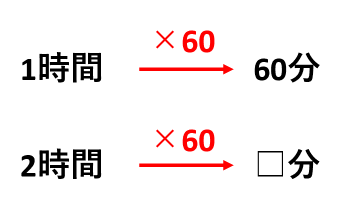
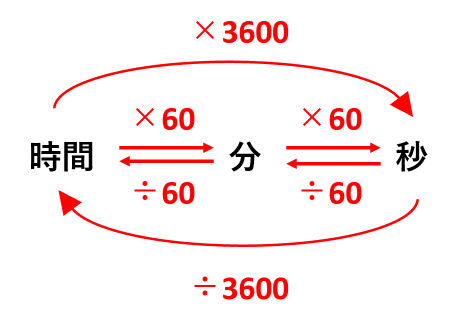
1時間が60分なので、「時間」を「分」に変換するときは、60をかければよいことがわかります。
- 2時間は2×60=120分
- 0.5時間は0.5×60=30分
- \(\frac{5}{3}\)分は\(\frac{5}{3}\)×60=100分
1分が60秒なので、「分」を「時間」に変換するときも、60をかけます。
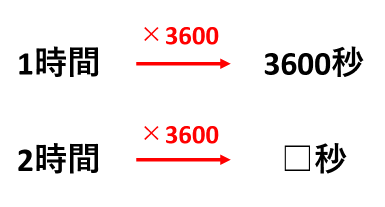
さらに、1時間が60分で、1分が60秒なので、1時間は3600秒です。したがって、「時間」を「秒」に変換するときは、3600をかけます。
- 2時間は2×3600=7200秒
- 0.5時間は0.5×3600=1800秒
- \(\frac{5}{3}\)分は\(\frac{5}{3}\)×3600=6000秒
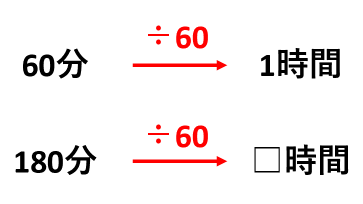
逆に、「分」を「時間」に変換するときは、60で割ります。
- 180分は180÷60=3時間
- 6分は6÷60=0.1時間
- 40分は40÷60=\(\frac{2}{3}\)時間
「秒」を「分」に変換するときも、60で割ります。さらに、「秒」を「時間」に変換するときは、3600で割ります。

時間と分と秒の関係は、下の図のようになる。ただ、この図を暗記するのではなく、その場で考えてわかるようにするのがおすすめだよ。
時刻から時間を引いてみよう
【例題1】のような引き算は、右側から(分→時間→日の順で)計算していきます。
24分から46分は引けません。こういうときは、「時(間)」から数字を借りてきます。ただし、時間と分の関係は60進法なので、1時間減らす代わりに60分増やします。

わかりにくければ筆算してみよう。24分に60を足すんだよ。100を足しちゃダメ!
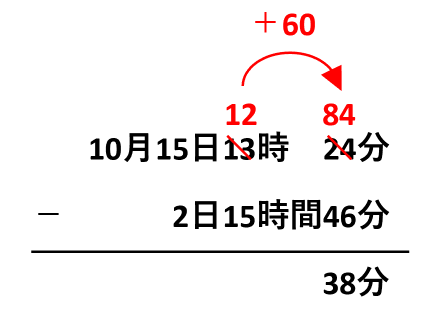
38分がわかったところで、「時」と「日」も計算します。
12時から15時間も引けないので、「日」から数字を借りてきます。ただし、24時制なので、1日減らす代わりに24時間増やします。

12時に24を足すのよ。60を足す場合と区別してね!
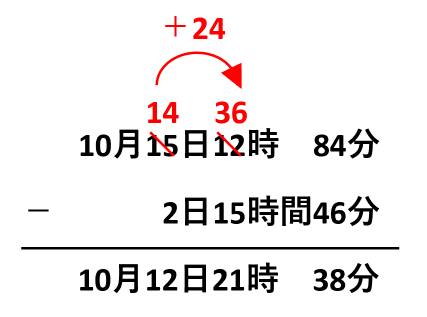
10月12日21時38分なので、問題文に合わせて10月12日午後9時38分が答です。
時間の四則計算をしよう
中学受験の時間の計算では、時間の四則計算が出ることがあります。
【例題2】□に当てはまる数を答えなさい。
(1) 3時間35分13秒-1時間29分8秒+46分57秒=□時間□分□秒
(2) 7時間53分46秒×5=□日□時間□分□秒
(3) 1日13時間48分÷9=□時間□分
(4) □時間□分□秒:52分25秒=7:5
(1)の解答(時間の足し算・引き算)
足し算と引き算が混ざっている計算では、足し算を先に計算すると楽です。
「81分」や「70秒」をそのままにして引き算をしました。最後に、62÷60=1あまり2なので62秒を1分2秒にして、分に繰り上げます。したがって、2時間53分2秒が答です。
(2)の解答(時間のかけ算)
それぞれの数字に5をかけていきます。
35÷24=1あまり11なので35時間は1日11時間、265÷60=4あまり25なので265分は4時間25分、230÷60=3あまり50なので230秒は3分50秒です。これらを足します。
(3)の解答(時間の割り算)
1日13時間÷9=37時間÷9=4時間で1時間あまります。この1時間を60分にして、60分+48分=108分なので、108分÷9=12分です。したがって、4時間12分が答です。
時間のわり算であまりをどうするかわからなくなるときは、一番小さい単位にそろえてから計算するとよいでしょう。
(3)では、単位を「分」にそろえて、1日13時間12分=1×24×60+13×60+48=2268分です。
2268分÷9=252分で、252÷60=4あまり12なので、4時間12分が答です。
(4)の解答(時間の比)
比の計算では、一番小さい単位にそろえて考えます。
52分25秒は52×60+25=3145秒なので、□時間□分□秒:52分25秒=△秒:3145秒=7:5より△=3145×7÷5=4403秒です。
4403÷60=73あまり23なので、4403秒は73分23秒です。さらに73÷60=1あまり13なので、73分は1時間13分です。したがって、1時間13分23秒が答です。
時間の計算は理科や社会でも必要
時間の計算は理科や社会でも必要です。算数でできるようにしておけば、他の科目でも困らなくなります。
問題集などで類題をたくさん解いて、時間の計算に慣れておきましょう。




コメント