つるかめ算の応用に「いもづる算」があります。
いもづる算が普通のつるかめ算とどう違うのかを理解した上で、その解き方を考えてみましょう。

個数の合計がわからないときはどうする?
【例題】1個30円のアメと1個40円のガムを30円の袋に入れて、代金の合計が1000円になるように買います。袋に入れたアメの個数は何通り考えられますか。
代金の合計から袋代30円を引いた970円がアメとガムの代金の合計です。
さて、【例題】は普通のつるかめ算と何が違いますか?
【例題】は、アメとガムの個数の合計がわかりません。代金の合計が970円になりさえすれば、アメとガムの個数はそれぞれ何個でもよいということです。
このように、個数の合計が1通りに決まっていない、つまり、答となる個数がいくつも出てくるタイプのつるかめ算を「いもづる算」といいます。いもづる算では、答となる個数の組を1組見つけてしまいます。
【例題】で、アメの個数を□個、ガムの個数を△個とすると、代金の合計は次の式で表されます。
この式に当てはまる□と△を「□=1、△=1のときは70円になって……」と一つ一つ考えるのは大変です。そこで、式を変形してヒントを探ります。
△は整数なので、(970-30×□)は40の倍数だとわかります。((970-30×□)が40で割り切れないと△は整数になりません)
□=1のとき、970-30×1=940で、これは40で割り切れません。
□=2のとき、970-30×2=910で、これも40で割り切れません。
□=3のとき、970-30×3=880で、これは40で割り切れます。したがって、アメ3個とガム22個で970円になります。
個数の合計を1通り見つけた後は、つるかめ算と同じように交換を考えます。いもづる算では、合計金額が変わらないように交換します。
【例題】では、アメ4個とガム3個が120円で等しくなります。したがって、ガム3個をアメ4個にどんどん交換していきます。これを表にすると次の通りです。
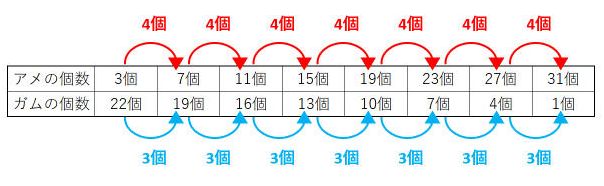
アメを4個増やすと、ガムが3個減ります。このようにアメとガムを交換していくと、アメの個数は8通りだとわかります。

アメ4個とガム3個が120円で等しくなるのはわかるんだけど、この4個と3個という組み合わせはどうやって見つけるんですか?

そもそも120円という金額はどこから出てきたと思う?

アメ1個の値段30円とガム1個の値段40円の最小公倍数ですか?

その通り!この最小公倍数120を30で割れば4、40で割れば3になるよね。だから、4個と3個なんだ。

整数で考える問題では、最小公倍数に着目するのがコツなんですね!
不定方程式も怖くない
いもづる算は、「いもづる式」という言葉が名前の由来です。
いものつるを引っ張るといもが次々と出てきます。これと同じように、いもづる式とは、一つの事実が明らかになったことをきっかけに、関係する事実が次々と明らかになっていくことです。
たとえば、犯罪捜査では、一人の犯人が捕まったことで共犯者が次々と捕まることを「いもづる式に逮捕」などといいます。
いもづる算でも、答となる個数の組が1組がわかれば、あとは交換していくことで、いもづる式に他の答もわかってしまいます。
ちなみに、いもづる算は、中学や高校の数学では「不定方程式」と呼ばれます。難しそうですが、やるべきことはいもづる算と変わりません。
いもづる算が解けるようになった中学受験生にとって、不定方程式は恐れるに足りません。
次の質問に答えましょう。(解答例は最後のページにあります)
・いもづる算はどのような手順で解きますか。




コメント