今回は、□を求める計算の中でも、□が2つある計算を解説します。まずは次の例題にチャレンジしてみましょう。
【例題】□に当てはまる数字を答えましょう。
(125-□)÷(62-□)=3\(\frac{1}{4}\)
線分図を描いてみよう
例題を解くのに役立つのが比と線分図です。
まずは、=の左側の割り算を分数にします。次に、=の右側の帯分数を仮分数にします。そうすると、もとの式は次のような「分数=分数」の形になります。割り算を見たら分数に直すという考え方が大切です。
「分数=分数」の式から、次の線分図を描けます。2本の線は分子と分母を表します。
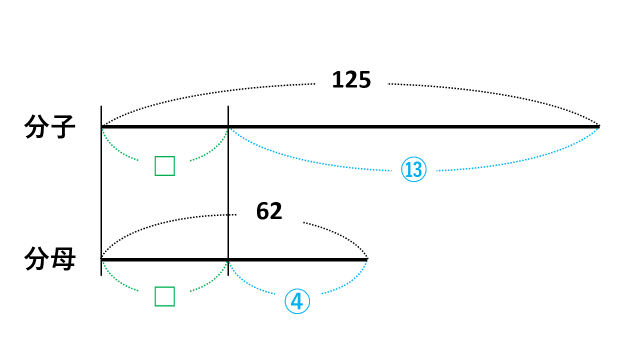
線分図を描くときのポイントは、□を線の左に寄せてしまうことと、=の右側の分数を比と考えて○で囲むことです。

□を線の左に寄せてしまうことと比を○で囲むことは、他の特殊算で線分図を描くときにも大切になるポイントだよ!
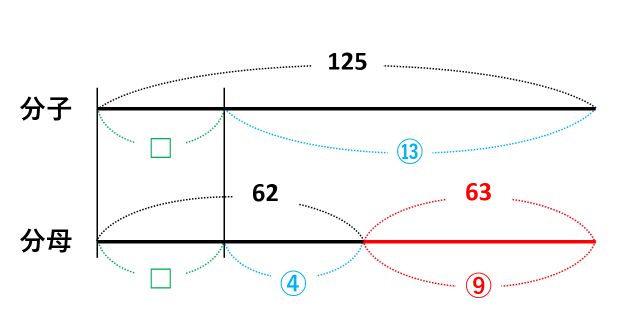
線分図の差に注目します。⑨=63なので①=63÷9=7です。分母に注目して、④=①×4=7×4=28なので□=62-④=62-28=34が答です。
比例式に書きかえよう
線分図よりも素直なのが、比例式に書きかえて考える解き方です。比例式とは、「A:B=C:D」という形の式です。
「A÷B(比の値)」は「A:B(比)」に書きかえられるので、例題の式も「÷」を「:」に書きかえましょう。
(125-□)÷(62-□)=13÷4
(125-□):(62-□)=13:4
この後は比例式の計算のきまり(外項の積=内項の積)に従って計算していきます。
(125-□)×4=(62-□)×13
分配法則を使って
125×4-□×4=62×13-□×13
500-□×4=806-□×13
□×13-□×4=806-500
□×9=306
□=306÷9=34
この計算がよくわからない場合は、線分図を描いて考えましょう。
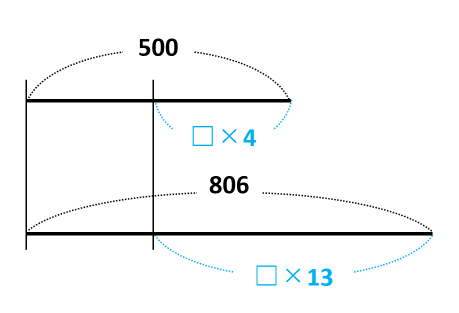
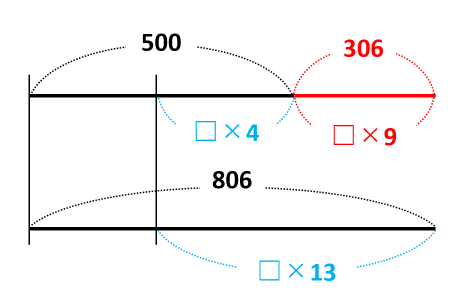
線分図の差に注目すると、□×9=306だとわかります。
比例式に書きかえる解き方は素直ですが、中学数学の方程式を知らない中学受験生は難しく感じるかもしれません。式を変形するのに慣れていないと線分図を描くことになり、最初から線分図を描く解き方よりも手間がかかります。この解き方は計算力に自信のある受験生向けです。

比例式では、125-□や62-□にカッコを付けないといけないんですか?

125-□にカッコを付けない125-□×4と、カッコを付けた(125-□)×4はそもそも別物だ。125-□×4は□に4をかけるだけだけど、(125-□)×4は125と□の両方に4をかけるんだよ。

15-3×4=15-12=3で、(15-3)×4=15×4-3×4=48ということですね。(15-3)×4は、カッコの中を先に計算すると12×4=48となって、分配法則を使って計算したときと同じ結果になるわ!
比と線分図が計算問題でも役立つ
比と線分図は、分配算や売買損益などの特殊算だけでなく、計算問題でも役立ちます。難しい計算に出会ったときは、「別の方法で式を表せないかな?」と考えてみることも大切です。
次の質問に答えましょう。(解答例は最後のページにあります)
① 割り算を見たら何をしますか。
② 線分図を描くときのポイントは何ですか。



コメント