割合は、中学受験の大手塾では4年で、公立小学校では5年で習います。しかし、イメージが湧きにくいのか、多くの小学生が苦手とします。
本記事では、割合の基本と線分図を使った問題の解き方をわかりやすく解説します。
「割合」「もとにする量」「くらべる量」とは?
「割合」というと、多くの小学生が「難しい!」と考えがちです。しかし、考え方自体は難しくありません。
まずは、身近な例から割合のイメージをつかみましょう。
12個のものをまとめて「1ダース」といいます。たとえば、鉛筆1ダースなら12本、消しゴム1ダースなら12個です。
このように12個(本)を1ダースとするならば、24個で2ダース、36個で3ダース……となります。
割合もダースの考え方と同じです。「ダース」を「倍」に置きかえて12個を「1倍」とすると、24個は2倍、36個は3倍……となります。
では、6個は12個の何倍でしょうか?
1倍の半分ですから、0.5倍か\(\frac{1}{2}\)倍です。
「倍」の考え方は2・3年で習います。4・5年で習う割合には「倍」がつきませんが、「倍」と同じ考え方です。
たとえば、「6個は12個の0.5(\(\frac{1}{2}\))です。」は「6個は12個の0.5倍(\(\frac{1}{2}\)倍)です。」という意味です。小数や分数でわかりにくいかもしれませんが、「12個は6個の2倍です。」と全く同じように考えられます。
割合とは、基準となる数を1(倍)としたとき、他の数がどのくらいになるのかを表すことです。
「6個は12個の0.5(\(\frac{1}{2}\))です。」では、12個を1にしているので、これが基準となる数です。このように基準となる数を「もとにする量」といいます。一方、6個は、基準となる12個とくらべています。このように基準となる数とくらべる数を「くらべる量(くらべられる量)」といいます。

「基準」という言葉の意味が分かりません。

たとえば、身長150cmは背が高いのかな?それとも低いのかな?

ええっと、私よりは背が高いけど、シイタケくんよりは低いですね。

今、エノキさんは「私よりは」「シイタケくんよりは」と言ったよね。この「~より」の「~」の部分を基準というんだ。いろいろなものを比べるとき、「大きい・小さい」「高い・低い」「良い・悪い」といった判断するためのもとになる数などが基準だ。

70点だけだと、点数が良いのか悪いのかがわかりません。もし平均点が60点なら70点でも点数が良いといえますが、平均点が80点なら点数が悪いといえます。このときの平均点が基準ってことですね!
割合・百分率・歩合の関係は?
単位のついていない割合や「倍」で表される割合は、もとにする量を1とします。一方、「%」で表される百分率は、もとにする量を100%とします。また、「割」「分」「厘」で表される歩合は、もとにする量を「10割」とします。
百分率や歩合を使う場合、もとにする量が1ではないことに注意しましょう。
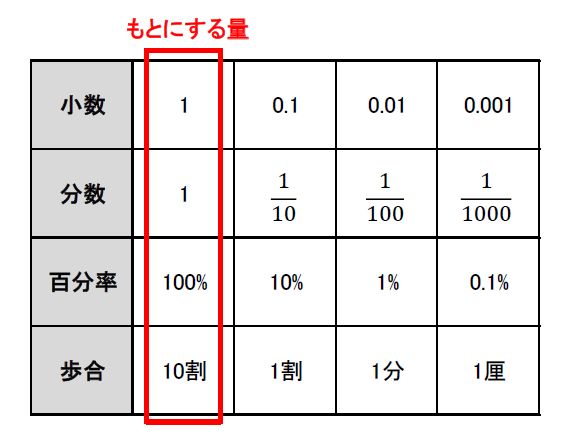
割合・百分率・歩合の関係は上の表のとおりです。たとえば、0.123と表された小数の割合は、百分率では12.3%、歩合では1割2分3厘と表されます。
もとにする量はどの数?
12個をもとにするとき、24個は2倍です。
このように書かれていれば、12がもとにする量だとすぐにわかります。
では、次のように書かれていたら、もとにする量はどの数でしょうか?
24個は12個の2倍です。
「もとにする」という表現が入っていない場合、まずは割合を見つけましょう。上の文では、「倍」がついている2が割合です。
割合を見つけたら、直前の「の」を見ます。この「の」は「をもとにすると」という意味なので、「の」の前にある数がもとにする量です。
上の文では12がもとにする量です。一方、24はくらべる量です。
線分図から読み取れる関係とは?
割合をイメージできたところで、実際に割合を線分図で表してみましょう。
24個は12個の2倍です。
この文を線分図で表すと次の通りです。
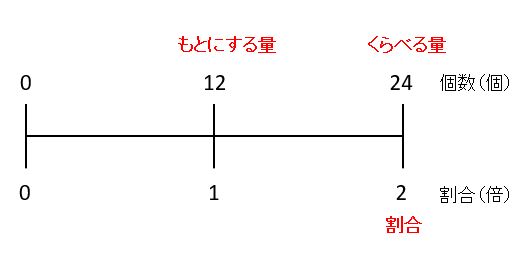
2が割合で、その直前の「の」の前にある12がもとにする量です。したがって、上に個数、下に割合を書いた線分図では、12の下に1を書きます。この1は問題文に書かれていませんが、必ず線分図に書き込んでください。
一方、割合の2は、くらべる量の24の下に書きます。
線分図では、もとにする量の下に1を、くらべる量の下に割合を書きます。
このように数値を書き込んだ線分図から、各数値の関係を考えてみます。すると、次のような比例関係に気づきませんか?
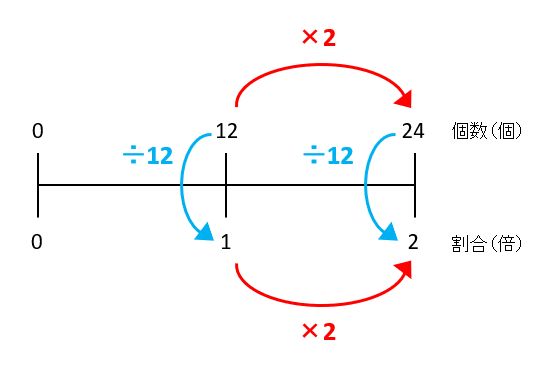
図の上に並んだ数と下に並んだ数(赤い矢印)を見比べます。左から右にどう変化しているのかを見ると、割合が2倍になると個数も2倍になります。上に並んだ数を式に表すと、24=12×2です。これは、「くらべる量=もとにする量×割合」の式に数値を当てはめたのと同じです。
逆に、右から左の変化を見ると、上に並んだ数の関係は12=24÷2です。これは、「もとにする量=くらべる量÷割合」の式に数を当てはめたものです。
今度は、左と右に並んだ数(青い矢印)を見比べましょう。上から下の変化を見ると、右に並んだ数値の関係は2=24÷12です。これは、「割合=くらべる量÷もとにする量」の式に数を当てはめたものです。
算数の問題集などには、割合の3公式が並んでいます。
- 割合=くらべる量÷もとにする量
- もとにする量=くらべる量÷割合
- くらべる量=もとにする量×割合
割合の3公式は、線分図から読み取れる関係を言葉で表したものです。線分図を正しく描ければ、わざわざ割合の3公式を暗記する必要はありません。
線分図を使って、実際に割合の問題を解いてみましょう。
割合を求める問題
□には単位が付いていないので割合です。□の直前の「の」の前にある30がもとにする量、18がくらべる量です。
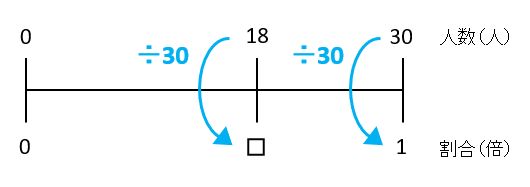
18にかけ算か割り算をすれば□を求められると見当をつけて、左と右に並んだ数値を見比べます。
右に並んだ数は、上から下に÷30をしています。したがって、左に並んだ数にも同じことをして□=18÷30=0.6となり、答は0.6です。
もとにする量を求める問題
割合は、「%」の付いている30です。30の直前の「の」の前にある□がもとにする量、12がくらべる量です。
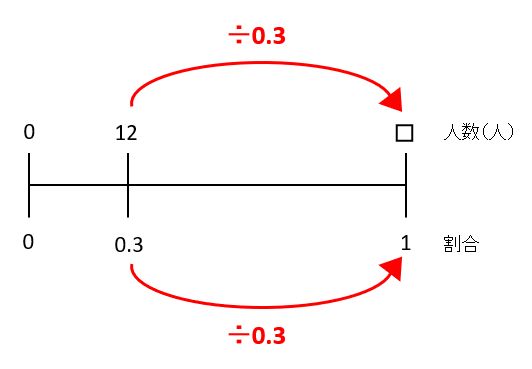
線分図では、計算しやすいように、百分率を小数の割合に直しました。100%は1、30%は0.3です。
12にかけ算か割り算をすれば□を求められると見当をつけて、上と下に並んだ数を見比べます。
下に並んだ数は、左から右に÷0.3なので、上に並んだ数にも同じことをして□=12÷0.3=40となり、答は40人です。
0.3を1にしたいときは÷0.3をしました。このように、ある数を1にしたいときは自分自身で割ります。これは、分数でも小数でも文字でも同じルールです。15÷15=1、3.14÷3.14=1、□÷□=1です。
くらべる量を求める問題
割合は、「%」の付いている70です。70の直前の「の」の前にある300がもとにする量、□がくらべる量です。
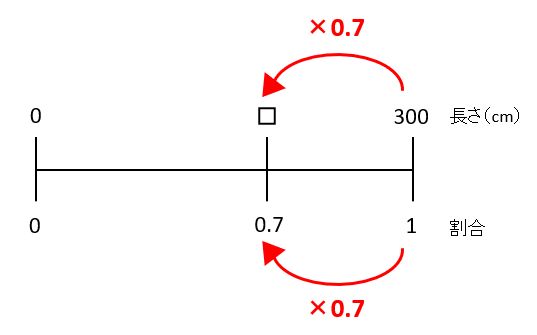
300にかけ算か割り算をすれば□を求められると見当をつけて、上と下に並んだ数値を見比べます。
下に並んだ数は、右から左に×0.7なので、上に並んだ数にも同じことをして□=300×0.7=210となり、答は210cmです。
「くもわ」の図に頼ると割合がわからなくなる
小学校や塾では、割合を教えるときに「くもわ」の図も教えるようです。「くもわ」の図とは、くらべる量・もとにする量・割合をテントウムシみたいに描いたものです。
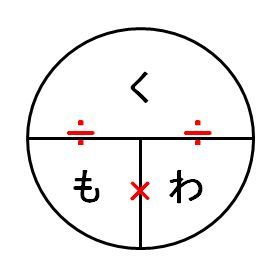
この図を使う場合、求めたい数の部分を手で隠して、残りの2つの数を式に表します。
たとえば、「□人の30%は12人です。」では、求めたい数がもとにする量なので、次のように「も」を手で隠します。
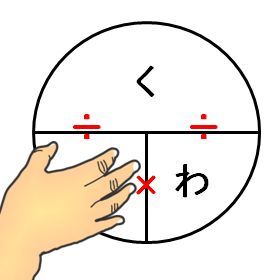
「も=く÷わ」とわかるので、これに数を当てはめて□=12÷0.3=40です。
「くもわ」の図は、答を出すだけなら便利です。しかし、この図に頼っていると、割合が何だか分からなくなってしまいます。できるだけ使わない方がいいでしょう。
割合の問題をいろいろな解き方で解いてみよう
勘の良い生徒ならば、線分図から「比を使えるのでは?」と気づくと思います。その気づきは正しいです。
たとえば、「300cmの70%は□cmです。」ならば、「□:300=0.7:1」や「□:0.7=300:1」が成り立ちます。これらの式を解いても□の値を求められます。結局、割合は比の仲間です。
「くもわ」の図を使って「できた!」と満足せず、「これを比で表すとどうなるかな?」などと考えられると、算数が楽しくなるでしょう。
次の質問に答えましょう。(解答例は最後のページにあります)
① 割合はどのようなことを表しますか。
② もとにする量とは何ですか。
③ 百分率や歩合とは何ですか。



コメント