三角錐を作って体積を求める！相似を利用して複雑な立体を単純化する

都立高校入試の過去問を使って、典型的な空間図形問題の解法について解説します。今回は、平成28年度の大問5を解いてみましょう。

最短距離を求める問題

[問1]のキーワードは、「ℓの値が最も小さくなる」です。「最も小さい（最小）」「最も短い（最短）」などを見たら、「直線」という言葉が思い浮かばなければアウトです。

図形問題で最短距離を求める場合、その距離は直線の長さになります。

とはいえ、[問1]では、Qでℓが折れ曲がっています。これを見て「どこにも直線が無い！」と決めつけてはいけません。空間図形で直線を考える場合、見取り図を展開図に書きかえます。

実際に、面ABEDと面ACFDをつなげた展開図を描いて、それに直線ℓを書き込みます。

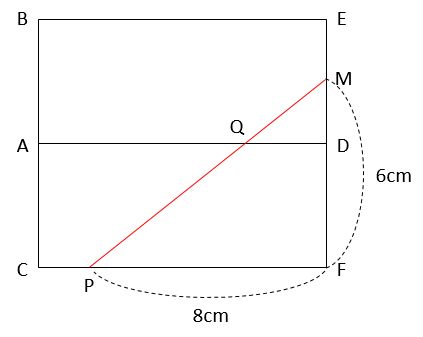
上図の通り、ℓは、∠MFP＝90°の直角三角形MFPの斜辺PMです。三平方の定理でℓの長さを求められます。

ℓ＝PM＝\(\sqrt{MF^2＋PF^2}\)

ℓ＝\(\sqrt{6^2＋8^2}\)＝\(\sqrt{100}\)＝10（cm）

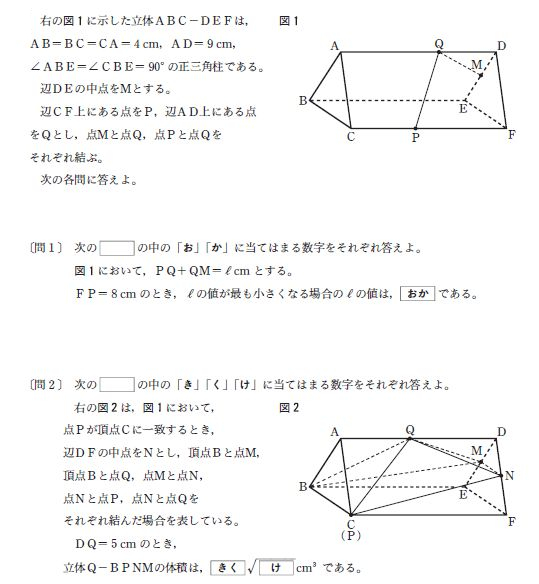
[問2]は、立体Q-BPNMの体積を求める問題です。

立体Q-BPNMは、底面を四角形BPNMにしたところで、高さを求められません。かといって、立体ABC-DEFから不要な立体の体積を引いていくのも無理そうです。なぜなら、立体MN-FEBCの体積を求められないからです。

こういう場合は、もう一度図形全体を観察してみましょう。すると、M、NがDE、DFのそれぞれの中点なので、中点連結定理からMNとEFが並行で、MNがEFの\(\frac{1}{2}\)倍です。これより、△DMN∽△DEFで△DEF≡△ABCなので、△DMN∽△ABCであることが分かります。

このように、平行な面に向きのそろった相似な図形がある場合、下図のように線分を延長します。

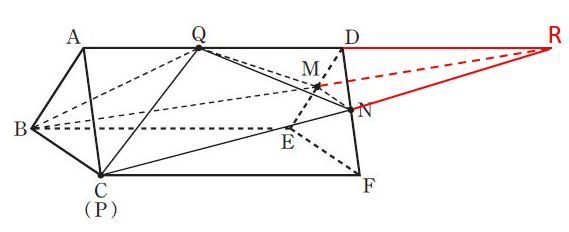
この図から分かる通り、AD、BM、CNを右側に延長した線は一点Rで交わります。そして、Rは、三角錐R-DMNと三角錐R-ABCの頂点です。

ここで、△DMN∽△ABCで相似比は1：2（＝MN：BC）なので、三角錐R-DMN∽三角錐R-ABCで相似比が1：2です。これをふまえて、図に数値を書き込んでいきます。

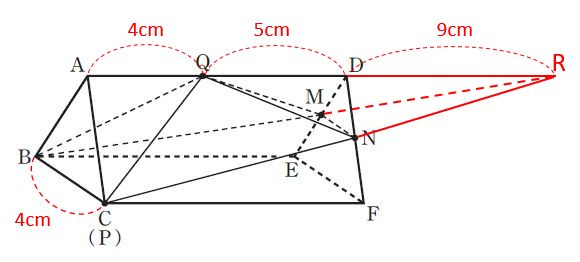
この図から、次の関係が分かります。

立体Q-BPNM＝三角錐R-ABC－（三角錐R-DMN＋三角錐Q-DMN＋三角錐Q-ABC）

それぞれの三角錐の体積を求めます。

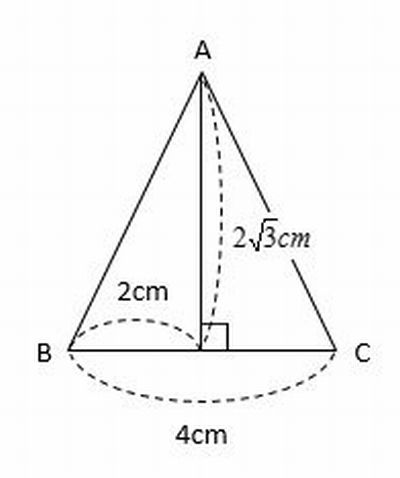
△ABCと△DMNは各三角錐の底面なので、次のようにして、それぞれの面積を求めます。

△ABC＝4×2\(\sqrt{3}\)×\(\frac{1}{2}\)＝4\(\sqrt{3}\)（cm²）

また、△DMN∽△ABCで、相似比は1：2なので、面積比は1：4である。

したがって、△DMN＝△ABC×\(\frac{1}{4}\)＝4\(\sqrt{3}\)×\(\frac{1}{4}\)＝\(\sqrt{3}\)（cm²）

必要な情報がそろったところで、立体Q-BPNMの体積を求めましょう。

立体Q-BPNM

＝三角錐R-ABC－（三角錐R-DMN＋三角錐Q-DMN＋三角錐Q-ABC）

＝△ABC×RA×\(\frac{1}{3}\)－（△DMN×RD×\(\frac{1}{3}\)＋△DMN×QD×\(\frac{1}{3}\)＋△ABC×QA×\(\frac{1}{3}\)）

＝4\(\sqrt{3}\)×18×\(\frac{1}{3}\)－（\(\sqrt{3}\)×9×\(\frac{1}{3}\)＋\(\sqrt{3}\)×5×\(\frac{1}{3}\)＋4\(\sqrt{3}\)×4×\(\frac{1}{3}\)）

＝\(\frac{\sqrt{3}}{3}\)×（72－9－5－16）

＝\(\frac{\sqrt{3}}{3}\)×42

＝14\(\sqrt{3}\)（cm³）

[問2]は、正答率が2.5%でした。ほとんどの受験生が解けなかった問題です。しかし、平行な面に向きのそろった相似な図形がある場合、線分を延長して相似な錐体を作るという解法を知っていれば、手に負えない問題ではないと思います。

今回解説した問題のように、最短距離の求め方や線分を延長する方法など、解き方を知らないと解けない問題が図形分野にはいくつもあります。

過去10年の都立高校入試問題を徹底分析して分野別にまとめた問題集「高校入試　虎の巻」でさまざまな問題に触れて、解き方をストックしていくことが大切です。

トップ画像＝Pixabay