2人が池の周りを歩く旅人算の中から、逆比を利用する応用問題を図を描きながらわかりやすく解説します。
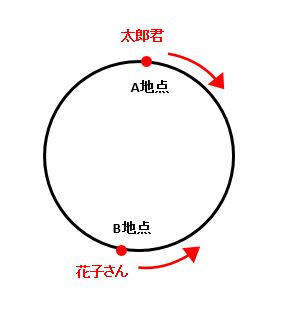
【例題】下の図のように、池を一周する道があります。この道のA地点から太郎君が、B地点から花子さんが、矢印の方向に向かって同時に歩き始めました。太郎君は出発してから6分後に初めて花子さんと出会い、その4分後にB地点を通過しました。さらに、A地点の少し手前で再び花子さんと出会い、その2分後にA地点に戻ってきました。太郎君と花子さんの歩く速さはそれぞれ一定であるとして、次の問いに答えなさい。
(1) 太郎君と花子さんの歩く速さの比を求めなさい。
(2) 太郎君がこの池を一周する時間は何分ですか。
線分図を描いて解いてみよう
池の周りを歩く問題では、円(池の絵)を描いて考える受験生が多いでしょう。
しかし、【例題】では太郎君と花子さんが池の周りを何周もするわけではないので、円よりも線分図の方が簡単です。
線分図は次のようになります。
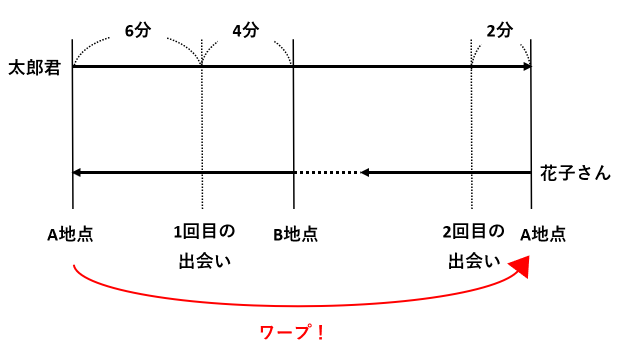
線分図は池を1周したときの道のりを表しています。円を切って伸ばした線分図なので、線分の両端がA地点です。
花子さんが左端のA地点に到着したら、右端のA地点にワープさせるのがポイントです。
問題文に書かれている時間(6分と4分と2分)を全て書きこんだところで、(1)から解いていきましょう。
(1)の解き方(速さの比を求める)
(1)では速さの比を求めます。しかし、問題文にある数字は時間だけです。そこで、道のりが一定ならば、速さの比は時間の比の逆比であることを利用します。
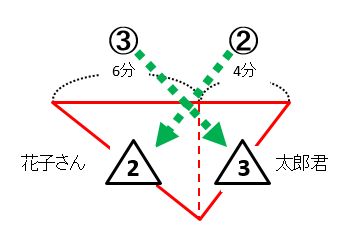
ここで、太郎君が4分で歩いた道のりを花子さんが6分で歩いたことに気づく必要があります。
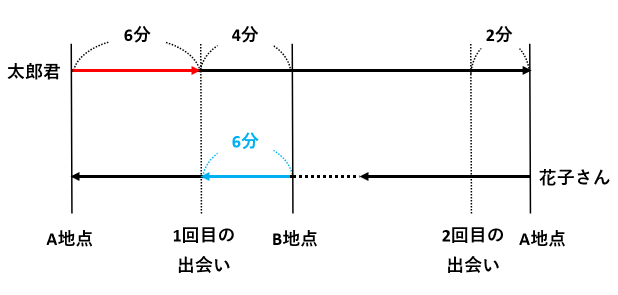
上の図で、太郎君は赤い矢印の道のりを6分で歩きました。このとき、花子さんは青い矢印の道のりを歩きました。2人が歩いた時間は同じなので、花子さんは青い矢印の道のりを6分で歩いたと考えられます。
一定の道のりを太郎君は4分で、花子さんは6分でそれぞれ歩いたので、時間の比は太郎君:花子さん=4:6=2:3です。
道のりが一定なので、2人の速さの比は太郎君:花子さん=3:2(時間の逆比)とわかります。
(2)の解き方(太郎君が一周する時間を求める)
(2)では、 太郎君が池を一周する時間を求めます。
まず、2人の速さの比は太郎君:花子さん=3:2なので、道のりが一定の線分を探して、逆比を利用しながら時間を書きこんでいきます。
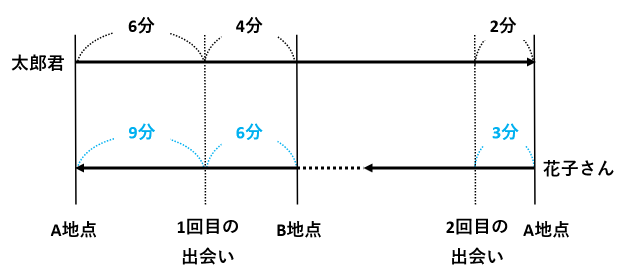
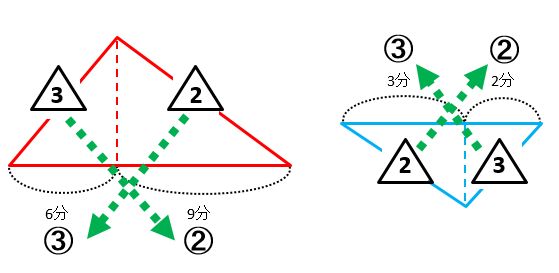
太郎君が6分で歩いた道のりを花子さんは9分で歩きます。また、太郎君が2分で歩いた道のりを花子さんは3分で歩きます。
次に、2人が1回目に出会ってから2回目に出会うまでに歩いた道のりを確認します。
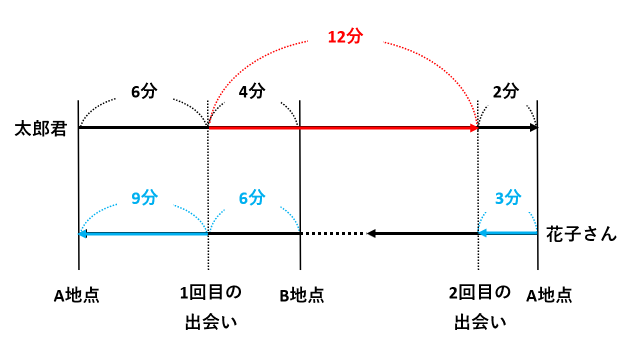
上の図で、2人が1回目に出会ってから2回目に出会うまで、太郎君は赤い矢印の道のりを歩き、花子さんは青い矢印の道のりを歩きました。2人は同じ時間を歩いているので、太郎君が歩いた時間は9+3=12分です。
したがって、 太郎君が池を一周する時間は6+12+2=20分です。
ダイヤグラムを描いて考えよう
線分図は、時間がゴチャゴチャしてわかりにくくなりがちです。もし混乱するなら、ダイヤグラムを描いてみるといいでしょう。
具体的には次のようなダイヤグラムになります。縦軸の両端をA地点としました。
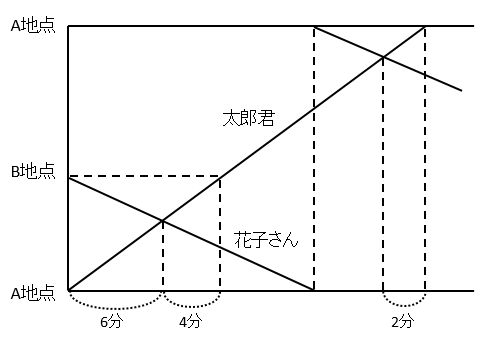
花子さんがグラフの下端(A地点)に到着したら、上端(A地点)にワープさせるのがポイントです。また、花子さんのグラフは全て平行になります。
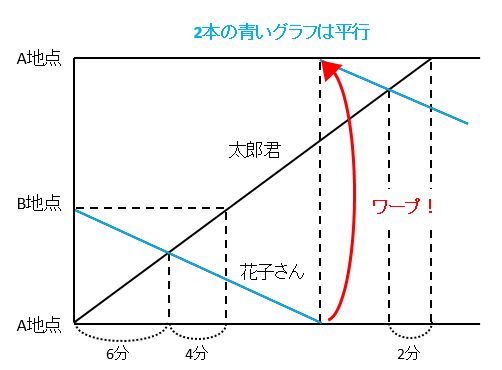
問題文中の「6分後」「4分後」から、太郎君のグラフの傾きが花子さんのグラフの傾きよりも急であることが分かります。傾きをまちがえて描くと、ダイヤグラムが原因で混乱します。
(1)の解き方(速さの比を求める)
(1)で速さの比を求めましょう。
道のりや時間で一定のものを探します。このとき、ダイヤグラムで三角形に注目するのがコツです。(1)では、下の赤い三角形に注目します。
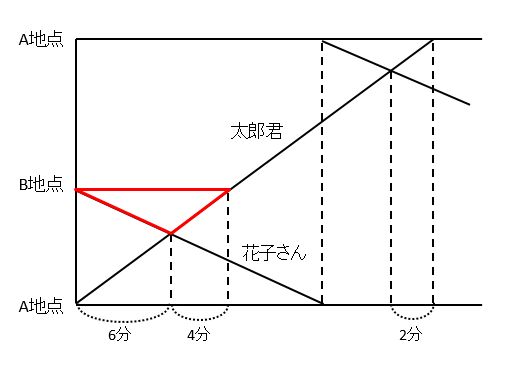
この三角形から、同じ道のりを歩く2人の時間の比は、太郎君:花子さん=4:6=2:3であるとわかります。
道のりが一定なので、2人の速さの比は太郎君:花子さん=3:2(時間の逆比)とわかります。
(2)の解き方(太郎君が一周する時間を求める)
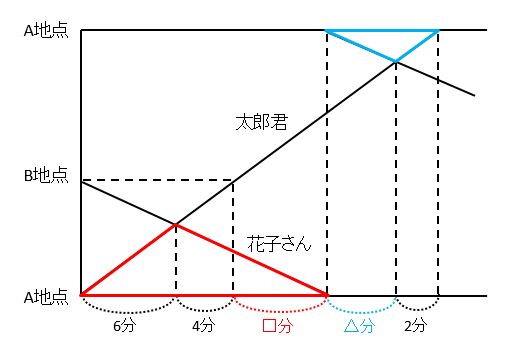
(2)で太郎君が池を一周する時間を求めるためには、下の図の□分と△分が必要です。そのために、左下の赤い三角形と、右上の青い三角形に注目します。
どちらの三角形も道のりが一定なので、時間の比と速さの比は逆比の関係です。(1)の結果から速さの比を書き込み、その逆比から□分と△分を求めます。
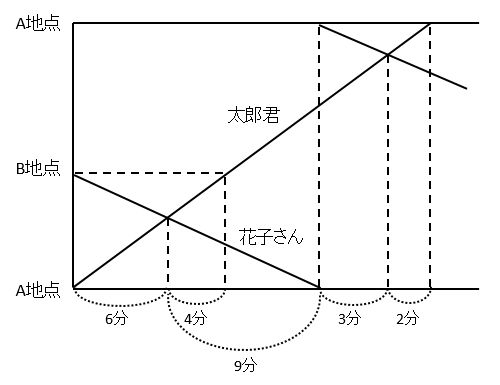
□(を含む時間)と△をダイヤグラムに書き込むと、太郎君が池を一周する時間も簡単に求められます。上の図より、太郎君が池を一周する時間は6+9+3+2=20(分)です。

線分図とダイヤグラムのどちらを使う?
2人が池の周りを歩く旅人算も、線分図やダイヤグラムを描くと解きやすくなります。
線分図は簡単に描けて、直感的にもわかりやすいのがメリットです。しかし、時間を考える問題ではゴチャゴチャして、却ってわかりにくくなることもあります。
一方、ダイヤグラムは、横軸で時間、縦軸で道のりを表すので、ゴチャゴチャすることはありません。しかし、正しく描けるようになるまで時間がかかるのがデメリットです。
問題によって線分図とダイヤグラムを上手に使い分けるといいでしょう。
トップ画像=Pixabay




コメント