問題演習コーナー
【問題】長さ8cmのテープを、のりしろを2cmとって下の図のようにつなげていきます。このとき、次の問いに答えましょう。
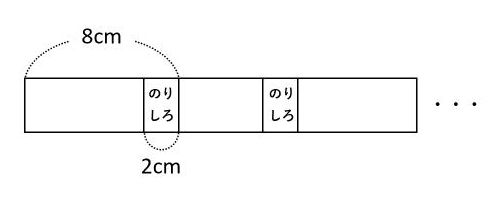
(1) テープを35枚つなげると、全体の長さは何cmになりますか。
(2) 全体の長さが350cmのとき、テープを何枚つなげましたか。
(1)の解答(全体の長さを求める)
有名なテープののりしろ問題です。実はこの問題も等差数列と考えることができます。
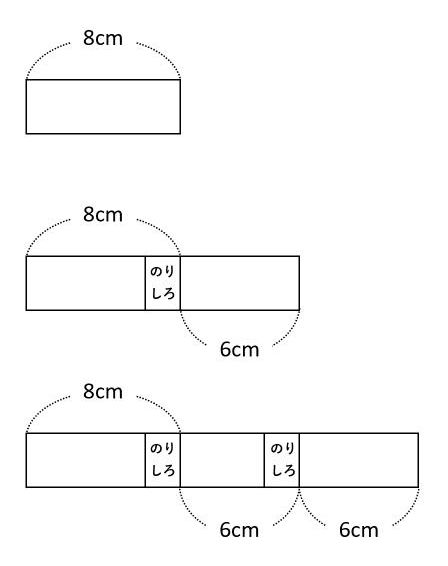
テープを1枚、2枚、3枚、…とつなげていくとき、全体の長さは8cm、14cm、20cm、…となります。8、14、20、…は、初めの数が8、加える数が6の等差数列です。
したがって、テープを35枚つなげると、全体の長さは8+6×(35-1)=212(cm)です。
別解(植木算の考え方)
植木算の考え方でも解けます。
のりしろをとらずにテープをつなげていくとすると、8×35=280(cm)の長さになります。
のりしろの数は、テープ1枚で0か所、テープ2枚で1か所、テープ3枚で2か所…なので、テープ35枚で34か所です。のりしろ34か所の長さは2×34=68(cm)です。
したがって、全体の長さは280-68=212(cm)になります。
(2)の解答(テープの枚数を求める)
テープを□枚つなげたとすると、全体の長さは8+6×(□-1)=350です。したがって、□=(350-8)÷6+1=58(枚)が答です。
別解(植木算の考え方)
テープを□枚つなげたとすると、のりしろは(□-1)か所なので、8×□-6×(□-1)=350です。これは、次のように計算します。
8×□-2×(□-1)=350
8×□=350+2×(□-1)
8×□=350+2×□-2
8×□-2×□=350-2
6×□=348
□=348÷6=58(枚)
植木算の考え方を使うと、(2)は計算が大変です。
① 等差数列は、どのような数列ですか。
(例)一定の数を次々に加えていった数列です。
② 等差数列のn番目の数を考えるとき、どのようなことを考えますか。
(例)「初めの数に『加える数』をいくつ足しているのか?」を考えます。
③ 数列の問題を考えるときに大切なのはどのようなことですか。
(例)いくつかの数から規則性を探ることです。
④ 等差数列の和を求めるとき、どのようなことをするといいですか。
(例)数列を逆順に並べることです。
トップ画像=Pixabay



コメント