中学受験算数で多くの受験生が苦手とする難問が群数列です。群数列とは、数列をあるきまりにしたがってグループ分けした数列です。
たとえば、2、4、6、8、10、12、14、…は、初めの数が2、加える数が2の等差数列です。この等差数列を2|4、6|8、10、12|14、…のように|で区切っていくと群数列になります。
今回は、群数列の問題で、何に注目して、どのように考えていけばいいのかを解説します。
等差数列が群数列になったらどうする?
【例題1】奇数を1から順に並べ、あるきまりにしたがって区切り、左から順に1組、2組、3組……とします。たとえば、7は3組の1番目の数で、15は4組の2番目の数です。
1|3、5|7、9、11|13、15、17、19|21、23、…
これについて、次の問いに答えなさい。
(1) 11組の11番目の数はいくつですか。
(2) 12組に並んでいる数の和はいくらですか。
奇数の列(初めの数が1、加える数が2等差数列)が群数列になったのが例題1です。このような群数列は、次の2つに注目しましょう。
① 各組に並んでいる数の個数
② 各組の最後の数
各組に並んでいる数の個数に注目しよう
まずは①から考えます。例題1では、各組に並んでいる数の個数は次の通りです。
1組 … 1の1個
2組 … 3、5の2個
3組 … 7、9、11の3個
4組 … 13、15、17、19の4個
このように書き出してみると、問題文の「あるきまり」が「各組に並んでいる数の個数が、1、2、3、4……という等差数列になっている」ことだとわかります。
例題1に限らず、群数列の問題では、各組に並んでいる数の個数も規則性のある数列になっています。このことをしっかり理解しましょう。
各組の最後の数に注目しよう
次に②を考えます。
例題1の(1)は「11組の11番目の数」すなわち「11組の最後の数」を求める問題なので、解いてしまいましょう。
各組の最後の数を求める場合、その数が数列全体で初めから何番目かを考えます。このとき、各組に並んでいる数の個数の和を利用します。
たとえば、例題1では、3組の最後の数である11は、数列全体では6番目の数です。この「6番目」は、1組と2組と3組に並んでいる数の個数の和1+2+3=6です。
同じように考えると、5は、1+2=3より、数列全体では3番目の数です。19は、1+2+3+4=10より、数列全体では10番目の数です。
さらに、「11組の11番目の数」すなわち「11組の最後の数」は、1+2+3+…+11=(1+11)×11÷2=66より、数列全体では66番目の数です。したがって、1+2×(66-1)=131が(1)の答です。

1+2+3+…+11=(1+11)×11÷2=66は、等差数列の和の公式を使ったんだね。1+2×(66-1)=131は、等差数列のn番目の数を求める公式だよ。

等差数列の公式については、以下の記事で確認してください。

ある組に並んでいる数の和を求めよう
(2)は、12組に並んでいる数の和を求める問題です。この問題では、12組に並んでいる数の個数、12組の最初の数と最後の数が必要です。
12組に並んでいる数の個数は12個です。
12組の最初の数は、(1)で求めた数に2を足せばいいので133です。
12組の最後の数は、133に2を11回足せばいいので、133+2×11=155です。
等差数列の和の公式を使って、(133+155)×12÷2=1728が(2)の答です。
分数の群数列にチャレンジしよう
【例題2】あるきまりにしたがって、下のように数を並べました。
1、\(\frac{1}{2}\)、\(\frac{1}{2}\) 、\(\frac{1}{3}\)、\(\frac{1}{3}\)、\(\frac{1}{3} \)、\(\frac{1}{4}\)、\(\frac{1}{4}\)、\(\frac{1}{4}\)、\(\frac{1}{4}\)、\(\frac{1}{5}\)、…
これについて、次の問いに答えなさい。
(1) 最初に出てくる\(\frac{1}{13}\)は、1番目から数えて何番目にありますか。
(2) 1番目から数えて108番目の数を求めなさい。
(3) 1番目から108番目までの数の和を求めなさい。
例題2の数列はグループ分けされていません。しかし、1が1個、\(\frac{1}{2}\)が2個、\(\frac{1}{3}\)が3個…という規則性があるので、次のようにグループ分けするといいでしょう。
1のグループを1組、\(\frac{1}{2}\)のグループを2組、\(\frac{1}{3}\)のグループを3組、…としていきます。n組には、\(\frac{1}{n}\)がn個並んでいます。
(1)の解答(最初に出てくる\(\frac{1}{13}\)の位置を求める)
各組に並んでいる数の個数は、1組に1個、2組に2個、3組に3個、…、12組に12個です。1組から12組までの個数の和は、等差数列の和の公式を使って、1+2+3+…12=(1+12)×12÷2=78です。したがって、最初に出てくる\(\frac{1}{13}\)は79番目にあります。
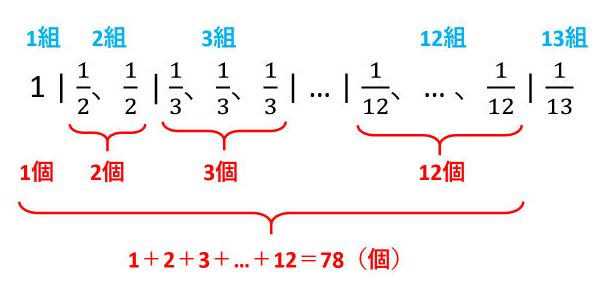
(2)の解答(1番目から数えて108番目の数を求める)
108番目の数が何組にあるのかを求めます。
108番目の数がある組の前の組を□組とします。1組から□組までに並んでいる数の個数の和は(1+□)×□÷2です。この和が108に最も近い値になる□を求めます。
(1+□)×□÷2=108
(1+□)×□=108×2=216
1+□を□にして□×□=216を考える。
14×14=196、15×15=225なので□=14と見当をつける。
(1+14)×14÷2=105<108
計算結果から、1組から14組までに並んでいる数の個数の和は105個です。108番目の数は15組の3番目にあるので\(\underline{\frac{1}{15}}\)が答です。
(3)の解答(1番目から108番目までの数の和を求める)
1組の数の和は1、2組の数の和は\(\frac{1}{2}\)+\(\frac{1}{2}\)=1、3組の数の和は\(\frac{1}{3}\)+\(\frac{1}{3}\)+\(\frac{1}{3}\)=1、…なので、各組の数の和はすべて1です。
1組から14組までの数の和は1×14=14です。
15組には106番目、107番目、108番目の数が並んでいるので、これらの和は\(\frac{1}{15}\)×3=\(\frac{1}{5}\)です。
したがって、1番目から108番目までの数の和は\(\underline{14\frac{1}{5}}\)です。
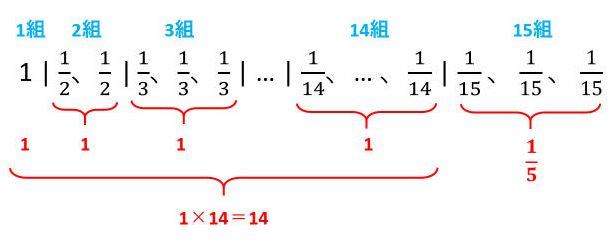

1組から3組の数の和をそれぞれ計算してみたら、すべて1になったわ。手を動かしていくつか計算してみると、何をすればいいかがわかるのよ。
群数列で他の受験生と差をつけよう
群数列では、何をすべきかを理解していないと、手も足も出なくなります。どんな群数列の問題でも、各組に並んでいる数の個数と各組の最後の数に注目することが大切です。
また、計算がゴチャゴチャしがちなので、途中計算や図などをしっかり書くといった、ミスをしないようにする工夫も求められます。
群数列を確実に解けるようになれば、他の受験生と差をつけられるはずです。
次の質問に答えましょう。(解答例は最後のページにあります)
① 群数列とはどのような数列ですか。
② 群数列の問題では何に注目しますか。
③ 各組の最後の数を求める場合、どのようなことを考えますか。




コメント
≪…群数列…≫を、カタチで分けて公式を観るのをミッケ・・・
1²+2²+3²+⋯+n²
=(1/6)n(n+1)(2n+1)
[ 『HHNI眺望』とは、4つの視座から観ようとするコト。
[H] ヒユーリスティック(heuristic)
ヒューリスティック(heuristic、Heuristik)または発見的(手法) とは、必ずしも正しい答えを導けるとは限らないが、ある程度のレベルで正解に近い解を得ることができる方法である。
[H] ホリスティック(holistic)
ホリスティック(Holistic)とは、ギリシャ語のholosを語源とし、全体・関連・つながり・バランスなどと訳されています。 ホリスティック医学では、身体だけでなく、目に見えない心や霊性を含めた<Body – Mind – Spirit>のつながりや、「環境」まで含めた全体的な視点で健康を考えます。 (ホリスティック自然数)
[N] ネスティング(nesting)
【入れ子 / ネスティング】とは、あるものの中に、それと同じ形や種類の(一回り小さい)ものが入っている状態や構造のこと。
[I] インターラクト(interact)
「interact」は「相互に作用する」「交流する」「相互に影響し合う」という意味 ]
この光景が、[ヒト]の誕生から、
母の日に臍を観つめてヒフミヨに
なり、
自然数のあるところ(n)までの[2乗の和](▢さん)を、△さん(nにする)と円(〇)を創っている正六角形と正三角形(△さん)とを[掛け算]の[ 【入れ子 / ネスティング】 ]に観る。
[自然数の2乗](n)を[△さん]とすると、次の[自然数の2乗]との和は、[凧形]( n(n+1) )に、この[凧形](2n)の2個に[凧形]の1個分の[光景](2n+1)に観える。
この[風景]が、[円](〇)と[正三角形](△)の6個とのインタラクト( [ 「interact」は「相互に作用する」] )と観る。
平方(2乗)で観る、数の言葉ヒフミヨ(1234)の自然数は、△さんの遍歴の姿が( n(n+1)(2n+1) )で、[円](〇)の一周という[1]の行為を[△]の[部分]の一周を[△]の6個で[全体]とすれば、[自然数のnまでの平方(2乗)の和]は、[全体]の[一周という行為]の[1/6]として[全体]を[部分]で[単位化](割るという行為)に観える。
ヒフミヨの〇の眺めは△に
割るコトは単位を創るヒフミヨに
√6意味知ってると舌安泰