ある事柄の起こり方全てを数え上げるのが「場合の数」です。その中でも、並び順を考える場合の数を「順列」といいます。今回は、異なるものを並べる順列の考え方について解説します。
順列の問題を解いてみよう
【例題】1、2、3、4、5の書かれた5枚のカードがあります。この5枚の中から3枚を選んで3けたの整数を作るとき、何通りの整数ができますか。
地道に数え上げる解き方と計算で答を求める解き方のそれぞれ考えてみましょう。
樹形図を描いて数え上げよう
まずは、地道に数え上げる解き方からです。
この解き方では、図や表などを使って、全ての場合を抜け漏れなく書き上げることが大切です。ここで役立つのが、全ての場合を枝分かれで描いた樹形図です。少し大変ですが、例題の樹形図は次の通りです。左から百の位、十の位、一の位としました。
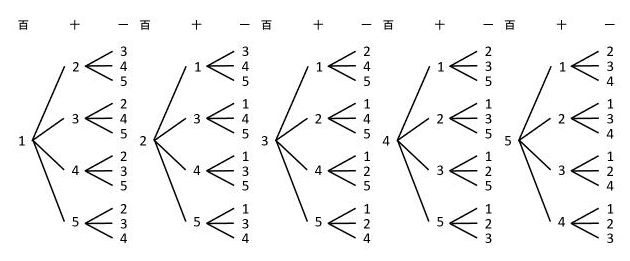
樹形図は、右側に枝が開いていくように描きます。
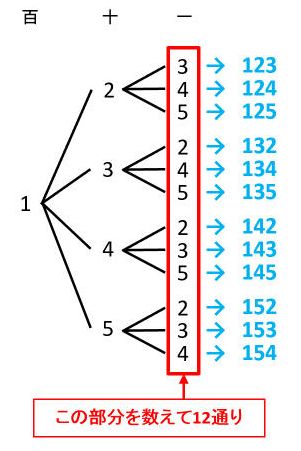
上の図では、1――2――3の枝は「123」で、1――5――4の枝は「154」です。
樹形図で場合の数を数える場合は、枝のいちばん右端(赤い枠で囲った部分)を数えます。今回の問題の答は、12×5=60(通り)です。
1で始まる樹形図を1つ描いた後、「同じ形のものが他に4つ描ける」と考えて12×5と考えてもいいでしょう。樹形図を全て描かなくても答は求められます。

次の【良い例】と【悪い例】はどこが違うかな?
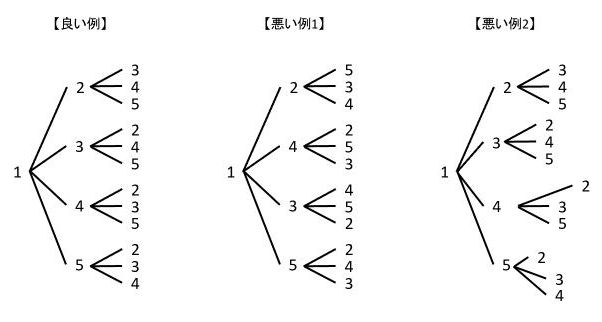

【良い例】は、上から下に、それから左から右に数字が大きくなっています。でも、【悪い例1】は、数字の並び方がメチャクチャです。

その通り!樹形図を描くときは、自分なりにルールを決めて並べるといいよ。数字ならば、「上→下と左→右の方向に小さい順で並べる」と決めておくと、数字が抜けたり同じ数字を何回も書いたりするのを防げるんだ。じゃあ、【悪い例2】は、どこがよくないかな?

数字が縦にそろっていないところですか?【良い例】と比べると、図が汚いです。

そうだね。樹形図は、縦に整然とそろえて書くことが大切だよ。縦にそろっていれば、パッと見で「ここはおかしい!」と気づけるからね。樹形図を描くときは、自分なりにルールを決めて規則的に描くことと、縦や横に数字などをそろえることを意識しよう。
積の法則から計算で答を求めよう
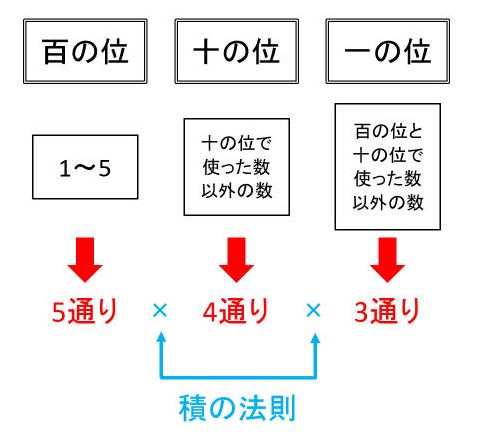
樹形図を見ると、百の位は1~5の5通りあります。ここで1を選ぶと、十の位が2~5の4通りあります。ここで2を選ぶと、一の位でさらに3~5の3通りあります。このように、百の位の5通りそれぞれについて十の位が4通りあり、その4通りそれぞれについて一の位が3通りあります。したがって、すべての場合の数は5×4×3=60(通り)と計算できます。これが積の法則です。
積の法則とは、事柄AとBについて、(AとBもどちらも起こる場合の数)=(Aが起こる場合の数)×(Bが起こる場合の数)が成り立つことをいいます。
Pや階乗の考え方を理解しよう
【例題】では、異なる5枚のカードから3枚選んで並べました。これは5P3と表されます(Pは「パーミュテーション」といいます)。同じようにして、異なるn個のものからr個を選んで並べる順列nPrは、積の法則から次のように書きかえられます(rはR(アール)の小文字です)。

Pを使うと、1~9の数字から3つを選んで3けたの整数を作る場合の数は、9P3=9×8×7=504(通り)と計算で求められます。並べるものが多い問題では、Pの考え方が役立ちます。
また、異なるn個のものすべてを並べる順列はn!(nの階乗)と表され、次のように書きかえられます。
階乗の公式に当てはめると、異なる5枚のカードすべてを並べる順列は5!=5×4×3×2×1=120(通り)です。
Pや階乗の使えるのは、並べるものがすべて異なるときだけです。同じものを含む順列では使えないので注意しましょう。
高校数学の公式も実は難しくない
Pや階乗は高校数学の公式なので、中学受験生は使いこなせなくても問題ありません。しかし、公式のもととなる考え方は理解する必要があります。
難しそうな公式の多くが、実は小学生でも理解できることを表しているだけだ、ということも覚えておくといいでしょう。
次の質問に答えましょう。(解答例は最後のページにあります)
① 樹形図を描くとき、どのようなことを意識するとよいですか。
② 積の法則では、どのようなことが成り立ちますか。



コメント