多くの中学生が「一次関数の利用」でつまずくのが動点問題です。
本記事では、長方形の周上を点Pが動く問題を通して、yをxの式で表すコツを紹介します。
点Pが長方形の周上を動く問題を解く
【問題】下の図は、AB=4cm、 BC=6cmの長方形ABCDで、点PはAを出発して毎秒2cmでA→B→C→Dの順で動く。点PがAを出発してからx秒後の△APDの面積をycm2とする。このとき、次の問いに答えなさい。
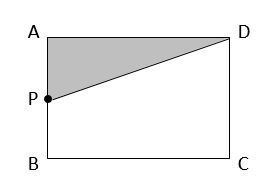
(1) 点Pが次の場合についてyをxの式で表しなさい。また、xの変域も求めなさい。
① AB上にある ② BC上にある ③ CD上にある
(2) xとyの関係をグラフに表しなさい。
(3) △APDの面積を8cm2となるのは、点PがAを出発してから何秒後か。
【問題】では、点Pの速さが毎秒2cmなので、Aを出発してからx秒後に点Pは2×x=2x(cm)動いたことになります。これは「速さ×時間=距離」を使った結果です。
一方、点PがBと重なるのは、「距離÷速さ=時間」より4÷2=2(秒後)です。Cと重なるのは、(4+6)÷2=5(秒後)です。
このように、動点問題では速さの考え方を使います。
yをxの式で表す問題
(1)では、点Pが①~③の場合について、それぞれyをxの式で表します。xの変域も必要なので、忘れずに求めなければなりません。
点PがAB上にある場合
△APDは下の図のようになります。
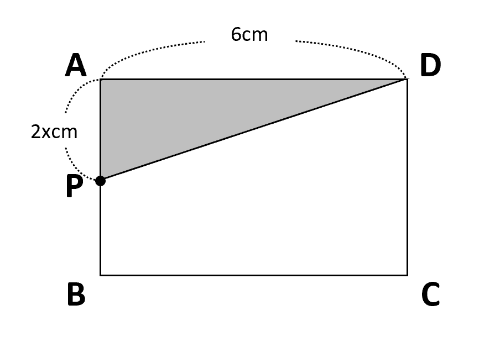
AP=2xcm、AD=6cmより、「三角形の面積=底辺×高さ×\(\frac{1}{2}\)」より△APD=2x×6×\(\frac{1}{2}\)=6x(cm2)なので、式はy=6xです。
また、点Pは0秒のときAと重なっていて、4÷2=2(秒後)にBと重なるので、xの変域は0≦x≦2です。
点PがBC上にある場合
△APDは下の図のようになります。
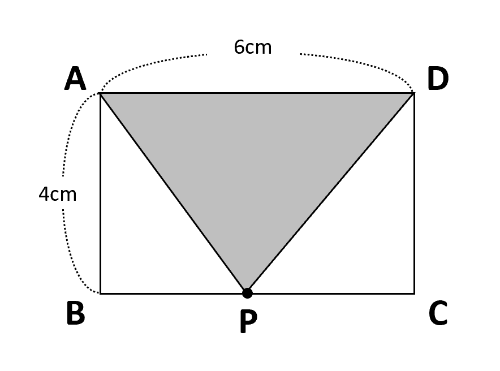
△APDの底辺をADとすると、点PがBC上のどこにあっても高さはABです。△APD=6×4×\(\frac{1}{2}\)=12(cm2)なので、式はy=12です。
また、点Pは2秒のときBと重なっていて、(4+6)÷2=5(秒後)にCと重なるので、xの変域は2≦x≦5です。
点PがCD上にある場合
△APDは下の図のようになります。
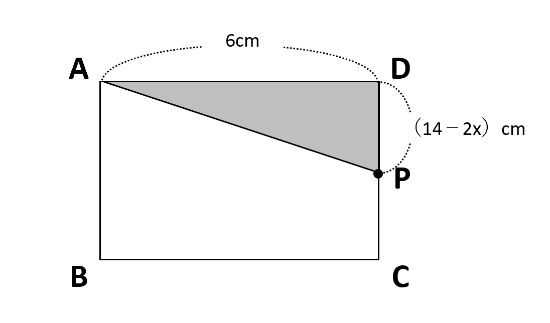
間違いやすいのはDPの長さです。下の図のように辺を一直線にすると、AB+BC+CD=4+6+4=14(cm)です。ここからAP=2xcmを引いてDP=14-2x(cm)を求めます。
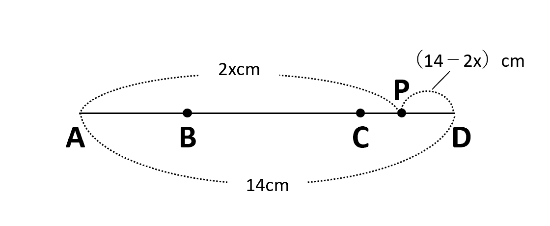
AP=14-2x(cm)、AD=6cmより、△APD=(14-2x)×6×\(\frac{1}{2}\)=-6x+42(cm2)なので、式はy=-6x+42です。
また、点Pは5秒のときCと重なっていて、(4+6+4)÷2=7(秒後)にDと重なるので、xの変域は5≦x≦7です。
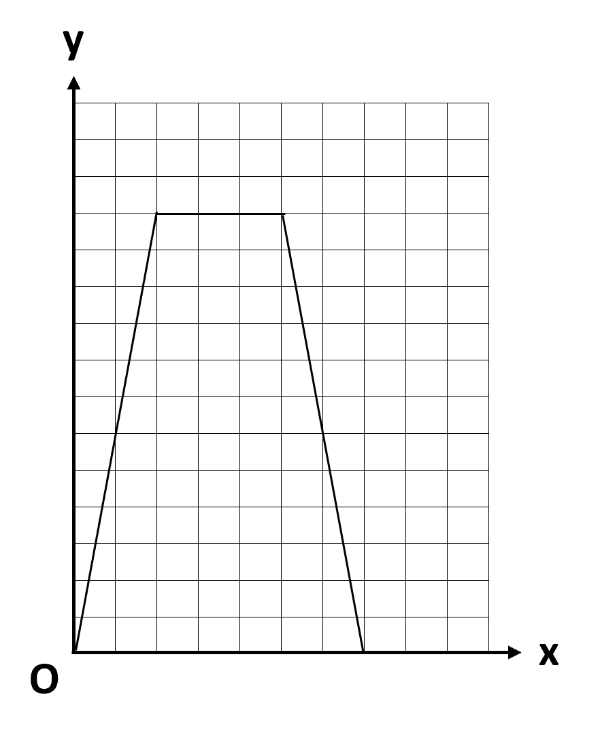
xとyの関係をグラフに表す問題
(2)では、xとyの関係をグラフに表します。このとき、(1)の①~③の変域でグラフを描くと、下のようになります。
時間を求める問題
(3)では、△APDの面積を8cm2となる時間を求めます。
まずは、グラフから時間を読み取れないかを確認しましょう。下の図を見る限り、y=8のときのxの値を読み取れません。
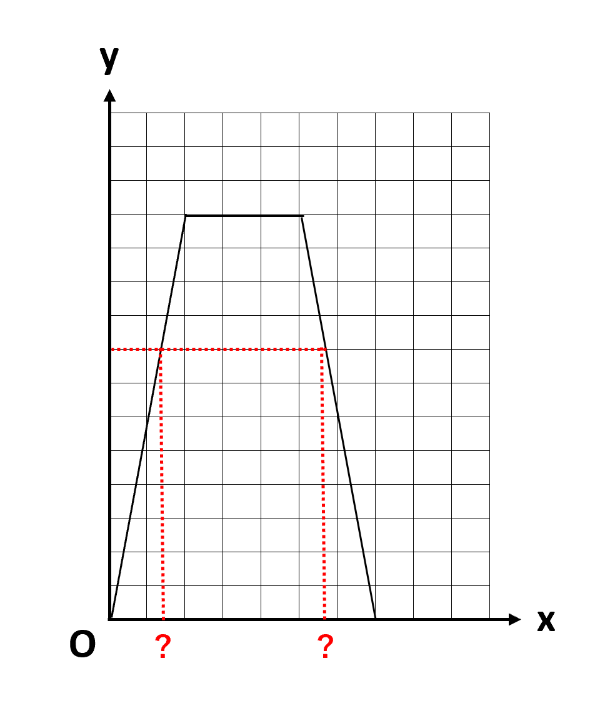
このような場合は計算でxの値を求めます。グラフからもわかる通り、y=8になるのは①の場合と③の場合の2回あるので、それぞれの式にy=8を代入します。
①の場合、y=6xにy=8を代入して8=6xよりx=\(\frac{8}{6}\)=\(\frac{4}{3}\)です。
②の場合、y=-6x+42にy=8を代入して8=-6x+42よりx=\(\frac{34}{6}\)=\(\frac{17}{3}\)です。
したがって、\(\underline{\frac{4}{3}}\)秒後と\(\underline{\frac{17}{3}}\)秒後が答えです。
グラフを描いてから式を求める
ここまでで紹介したのは、式を求めてからグラフを描く解き方です。これだと、式を間違うとグラフを描けません。
発想を転換して、グラフを描いてから式を求めてみましょう。
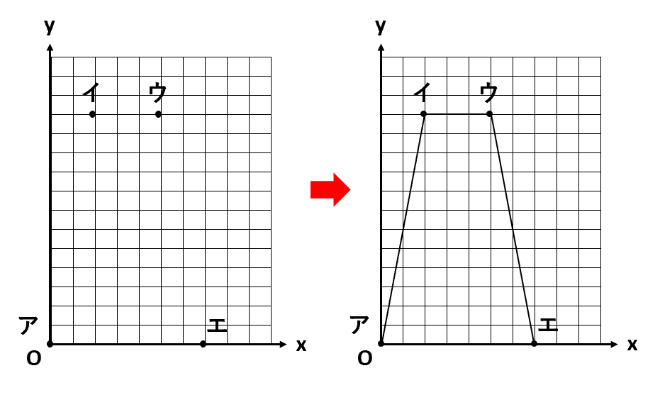
動点が頂点と重なる場合の座標を求める
グラフを先に描くときは、動点が頂点と重なる場合の座標を求めるのがポイントです。
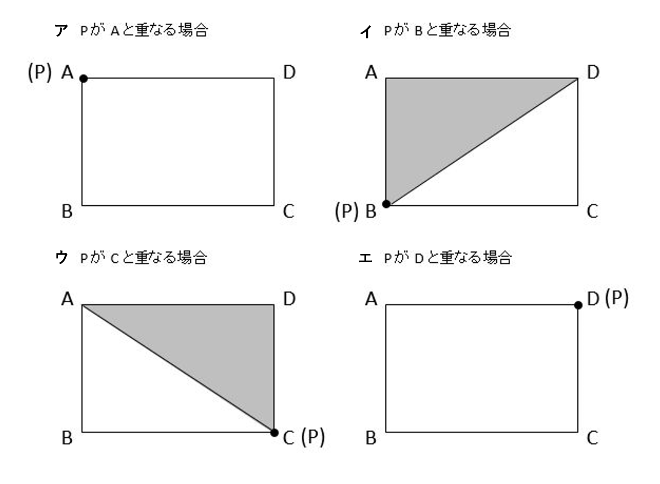
それぞれの場合について、Pの移動時間xと△APDの面積yを求めます。
アの場合、Pは動いていないので、移動時間は0秒、すなわちx=0です。また、△APDができていないので、その面積は0cm2、すなわちy=0です。これより、座標は(0、0)です。
イの場合、PはAB=4cmを動いたので、移動時間は4÷2=2(秒)、すなわちx=2です。また、△APDの面積は4×6×\(\frac{1}{2}\)=12(cm2)、すなわちy=12です。これより、座標は(2、12)です。
ウの場合、PはAB+BC=10cmを動いたので、移動時間は10÷2=5(秒)、すなわちx=5です。また、△APDの面積は4×6×\(\frac{1}{2}\)=12(cm2)、すなわちy=12です。これより、座標は(5、12)です。
エの場合、PはAB+BC+CD=14cmを動いたので、移動時間は14÷2=7(秒)、すなわちx=7です。また、△APDができていないので、その面積は0cm2、すなわちy=0です。これより、座標は(7、0)です。
点を打ってグラフを描く
まず、ア(0、0)、イ(2、12)、ウ(5、12)、エ(7、0)の各点を打ちます。
次に、ア~エの点を結びます。動点が1つで、その動点の速さが一定のときは、点と点を直線で結びましょう。曲線や折れ線になることありません。
先に(2)が終わりました。
グラフから式を求める
ア~イ、イ~ウ、ウ~エの3か所で直線の式をそれぞれ求めます。
ア~イでは、xの増加量が2のときyの増加量が12なので、直線の傾き(変化の割合)は\(\frac{12}{2}\)=6です。直線は原点を通るので切片は0となり、直線の式はy=6xです。xの変域はグラフから0≦x≦2と読み取れます。
イ~ウでは、yが12からずっと変わりません。したがって、直線の式はy=12です。xの変域はグラフから2≦x≦5と読み取れます。
ウ~エでは、xの増加量が2のときyの増加量が-12なので、直線の傾き(変化の割合)は\(\frac{-12}{2}\)=-6です。直線の切片をbとして、直線の式はy=-6x+bと表せます。これがエ(7、0)を通るので、0=-6×7+bよりb=42となり、直線の式はy=-6x+42です。xの変域はグラフから5≦x≦7と読み取れます。
以上より、(1)の式とxの変域は① y=6x(0≦x≦2)、② y=12(2≦x≦5)、③ y=-6x+42(5≦x≦7)です。
(3)の解き方は上と同じなので省略します。
関数の問題はグラフを描いて考える
一次関数や二次関数などの問題では、グラフを描いて考えることが大切です。本記事で紹介した動点問題のように、いくつかの座標を求めてから、「これらの点を通るグラフはどうなるのだろう?」と考えてみるのもよいでしょう。



コメント