時計の長針と短針が作る角度やその角度になる時刻を求める問題が「時計算」です。
本記事では、時計算の解き方をわかりやすく解説します。
時計算は追い越しの旅人算
旅人算は速さの応用問題です。そのため、時計算でも道のり・速さ・時間が大切になります。ただし、時間以外の道のりと速さに当たるものは旅人算と違います。
時計算で道のりに当たるのは、長針と短針が作る角の大きさです。速さに当たるのは、長針と短針が1分間に動く角の大きさで、「角速度」と呼ばれます。
長針は、1時間=60分で文字盤を一周して同じ位置に戻ってきます。したがって、長針の角速度は、360°÷60分=毎分6°です。
一方、短針は、1時間=60分で30°(360°÷12時間)動きます。したがって、短針の角速度は、30°÷60分=毎分0.5°です。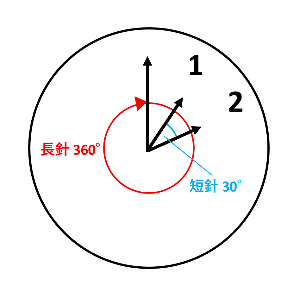
長針と短針が作る角の大きさを求める
長針と短針の角速度がわかったところで【例題1】を解いてみましょう。
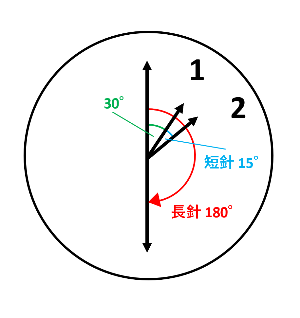
下の図から、1時から1時30分までの30分間で、長針は毎分6°×30分=180°、短針は毎分0.5°×30分=15°動きます。したがって、求める角の大きさは180°-30°-15°=135°です。

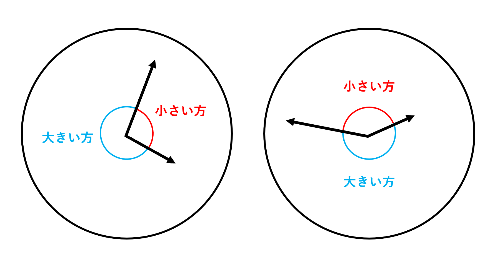
時間によって、どこが小さい方の角になるかが変わるから注意してね。
角の大きさから時刻を求める
逆に、【例題2】は、どのように解けばいいのでしょうか?
【例題2】では、長針と短針の動きを図で表しましょう。
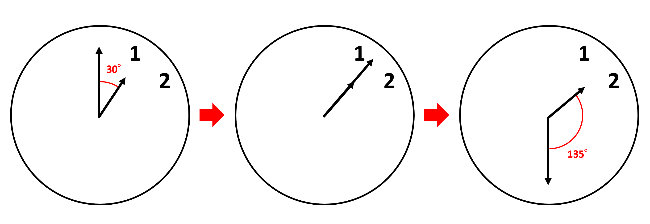
1時で長針と短針は30°離れています。長針と短針は1分で6°-0.5°=5.5°=\(\frac{55}{10}\)°=\(\frac{11}{2}\)°ずつ近づいていって、ある時刻で重なった後、\(\frac{11}{2}\)°ずつ離れていって135°になります。
(30°+135°)÷毎分\(\frac{11}{2}\)°=30分なので、はじめて時計の長針と短針の角度が135°になる時刻は確かに1時30分です。

「はじめて時計の長針と短針の角度が135°になる」とあるけれど、「2回目に時計の長針と短針の角度が135°になる」時刻もあるんだ。(30°+225°)÷毎分\(\frac{11}{2}\)°=46\(\frac{4}{11}\)分なので、2回目に135°になる時刻は1時46\(\frac{4}{11}\)分だね。必ずしも11で割り切れるとは限らないよ。
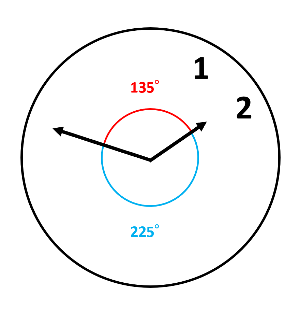
時計算は長針と短針の角速度の差を使うので、追い越しの旅人算と同じと考えられます。
長針と短針が作る角の大きさは?
【例題3】2時と3時の間で、時計の長針と短針が作る角の大きさについて、次の問いに答えなさい。
(1) 長針と短針が重なるのは2時何分ですか。
(2) 長針と短針が反対の方向に一直線に並ぶのは2時何分ですか。
(3) 長針と短針の作る角の大きさが2回目に30°になるのは2時何分ですか。
(1)の解答(長針と短針が重なる時刻を求める)
長針と短針の動きを図で表しましょう。
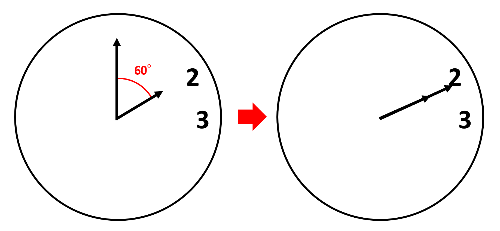
2時で、長針と短針は60°離れています。長針と短針は1分で\(\frac{11}{2}\)°ずつ近づいていって、ある時刻で重なります。この時刻は、60°÷毎分\(\frac{11}{2}\)°=10\(\frac{10}{11}\)分から、2時10\(\frac{10}{11}\)分です。
(2)の解答(長針と短針が反対の方向に一直線に並ぶ時刻を求める)
(1)の後の長針と短針の動きを図で表しましょう。長針と短針が反対の方向に一直線に並ぶのは、長針と短針の作る角度が180°のときです。
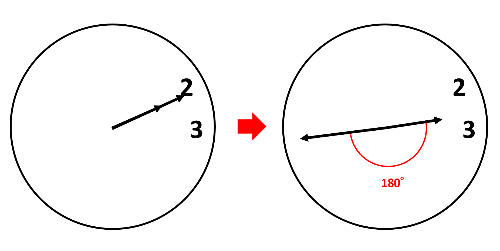
2時から考えるなら、(60°+180°)÷毎分\(\frac{11}{2}\)°=43\(\frac{7}{11}\)分なので、2時43\(\frac{7}{11}\)分が答えです。
(3)の解答(長針と短針の作る角の大きさが2回目に30°になる時刻を求める)
長針と短針が1回目に30°になるのは(1)の時刻の前です。2回目に30°になるのは(1)の時刻の後です。これをふまえて、(1)の後の長針と短針の動きを図で表しました。
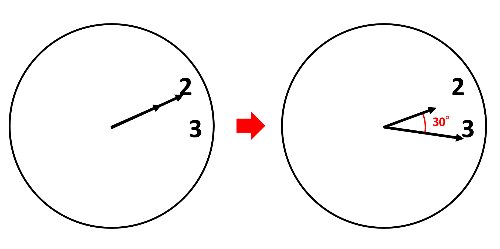
2時から考えるなら、(60°+30°)÷毎分\(\frac{11}{2}\)°=16\(\frac{4}{11}\)分なので、2時16\(\frac{4}{11}\)分が答えです。
次の質問に答えましょう。(解答例は最後のページにあります)
・時計算で使う\(\frac{11}{2}\)はどのような数ですか。




コメント