つるかめ算は、中学受験を志す小学生が3、4年で学ぶ特殊算です。
つるかめ算とは、足の数が異なるつるとかめについて、足の数の合計と匹数の合計からそれぞれの匹数を求める問題です。つるとかめは、ノートと鉛筆、50円切手と80円切手など、値段の異なるものになることもあります。
つるかめ算を“公式”で教えてしまう塾も多いようです。しかし、“公式”だけを覚えた受験生は、少し設定の変わったつるかめ算に太刀打ちできず……。
そうならないように、今回は、つるかめ算の基本をさまざまな角度から紹介します。
つるかめ算の基本は仮定と交換
【例題】つるとかめが合わせて15匹います。足の数は合わせて42本です。つるとかめはそれぞれ何匹いますか。
例題は、典型的なつるかめ算の問題です。このタイプの問題では、つるかかめのどちらか一方しかいないと仮定するのがポイントです。
15匹すべてがかめだと仮定しよう
15匹すべてがかめだと仮定します。このとき、足の数の合計は4×15=60(本)になります。しかし、実際の足の数は42本。60本と42本の差である18は、どのように考えればいいのでしょうか?
そもそも15匹すべてがかめだと仮定しているため、実際の問題文とは矛盾します。そこで、かめ1匹をつる1匹と交換すると、足の数は2本減ります(つるを数える場合、「1羽」のように「羽」を用いますが、わかりやすく「匹」で統一します)。
同じように考えて、かめ2匹をつる2匹と交換すると、足の数は4本減ります。
このように、交換したときに減る足の数の和が18になるということです。ここまで理解できれば、18÷2=9(匹)がつるの匹数だとわかります。かめの匹数は15-9=6(匹)です。
15匹すべてがつるだと仮定しよう
15匹すべてがつるだと仮定します。このとき、足の数の合計は2×15=30(本)で、実際の足の数との差は42-30=12です。
つる1匹をかめ1匹と交換すると、足の数は2本増えます。したがって、交換したときに増える足の数の和が12です。かめの匹数は12÷2=6(匹)、つるの匹数は15-6=9(匹)です。

そもそも「仮定」って何ですか?

仮定は、事実とは関係なく、「もし~ならば」と決めることだよ。たとえば、今晴れているけれど「もし雨が今降っていたならば、お出かけは中止だった」というとき、「もし雨が今降っていたならば」の部分が仮定だね。
つるかめ算を表・面積図・消去算で解こう
仮定と交換の考え方が分かっていれば、つるの匹数は(60-42)÷(4-2)=9(匹)、かめの匹数は(42-30)÷(4-2)=6(匹)と求められます。
この式の作り方を“公式”として教わった受験生もいるはずです。しかし、多くの受験生はこの“公式”の意味をわかっていませんし、使いこなせていません。
そんな受験生は、変な“公式”に頼るのではなく、表や面積図などを使って考えられるようにするといいでしょう。
表を書いて情報を整理しよう
つるかめ算に限らず、算数では表を書いて情報を整理することが大切です。
15匹すべてがかめだと仮定したときの表は次の通りです。
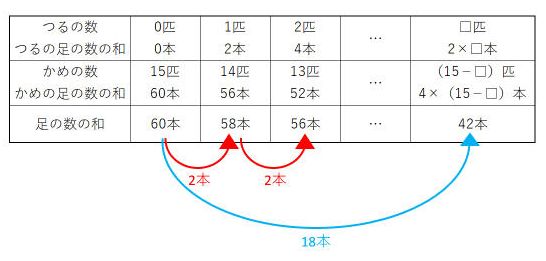
表から、つるを□匹とすると、□=18÷2=9(匹)と求められます。かめの匹数は15-9=6(匹)です。
以上で答を求められましたが、15匹すべてがつるだと仮定したときの表も書いてみましょう。
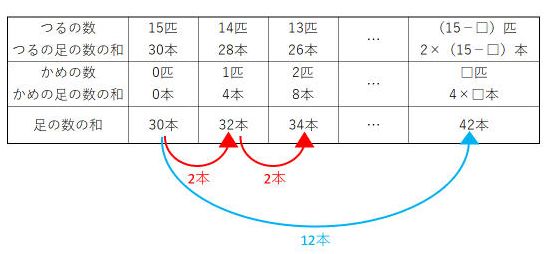
表から、かめを□匹とすると、□=12÷2=6(匹)と求められます。つるの匹数は15-6=9(匹)です。
面積図を使って図形的に考えよう
「つる1匹の足の数は2本」「かめ1匹の足の数は4本」のように、「1」あたりの数のことを「単位量あたりの大きさ」といいます。
単位量あたりの大きさを利用する問題では、「面積図」と呼ばれるツールを使うと解きやすくなります。
つるかめ算では、大小2つの長方形をくっつけた面積図を描きます。まずは、それぞれの辺や面積の意味を理解しましょう。
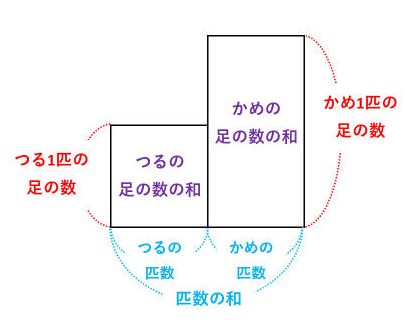
これに実際の数値を当てはめると次の図になります。
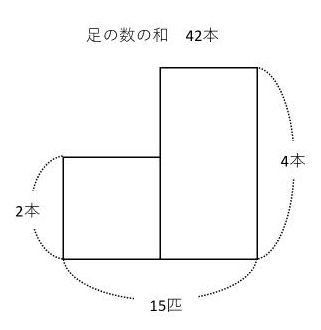

長方形の縦に単位量当たりの大きさを書くといいのね!
15匹すべてがかめだと仮定すると、面積図は次のようになります。
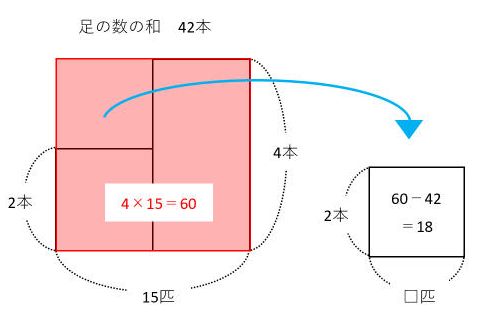
図の左上にできた長方形に着目して、□=18÷2=9(匹)となります。□はつるの匹数なので、つるが9匹、かめが6匹とわかります。
以上で答を求められましたが、15匹すべてがつるだと仮定したときの面積図も書いてみましょう。
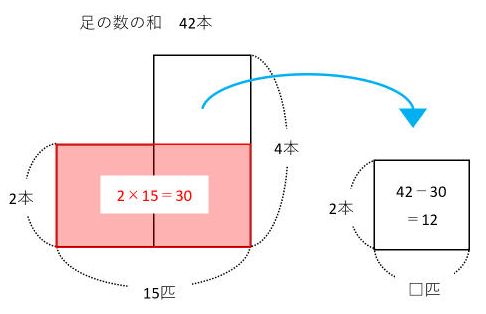
図の右上にできた長方形に着目して、□=12÷2=6(匹)となります。□はかめの匹数なので、つるが9匹、かめが6匹とわかります。
表を長方形で表したのが面積図です。一見すると図形とは無関係な問題を図形的に処理できるという発想がおもしろいのではないでしょうか?
消去算を使って計算で答を求めよう
つるかめ算では、仮定と交換をきっちり理解した上で、表に整理したり面積図を描いたりすることが大切です。
しかし、このような王道の解法をどうしても理解できない受験生がいます。そんな受験生は消去算を使って計算するといいでしょう。

つるを□匹、かめを△匹とする。
匹数の合計 □+△=15 … ①
足の数の合計 2×□+4×△=42 … ②
①×2 2×□+2×△=30 … ③
②-③ 2×△=12
したがって、△=12÷2=6(匹) … かめの匹数
また、□=15-6=9(匹) … つるの匹数
表や面積図を使いこなせる受験生も、つるかめ算を消去算で解いてみると、新たな発見があるはずです。
つるかめ算を後回しにしても大丈夫
小学校中学年だと、つるかめ算を論理的に考えるのはまだまだ難しいのではないでしょうか?
「つるかめ算がよくわからない」という小学3、4年生は、無理につるかめ算を理解しようとしなくても大丈夫です。つるかめ算を後回しにして、先に計算問題や図形問題などを進めていくといいでしょう。
今わからなくても、将来必ずわかるときが来ます。そのときにもう一度つるかめ算に挑戦してみてください。
次の質問に答えましょう。(解答例は最後のページにあります)
① つるかめ算ではどのようなことを仮定しますか。
② 面積図はどのような問題で役に立ちますか。
③ つるかめ算では面積図の長方形の縦と横にはそれぞれ何を書きますか。





コメント