お母さんに買い物を頼まれた太郎君は、近所のスーパーでリンゴとミカンを買いましたが、渡された金額よりも少ない代金になりました。なぜでしょうか?
値引きされていたのでなければ、それぞれの個数をまちがえて買ったと考えられます。
中でも多いのがとりちがえです。1個100円のリンゴ7個、1個40円のミカン4個を買うつもりが、リンゴ4個、ミカン7個買ってしまったら、860円が680円になってしまいます。
差集め算では、このようなとりちがえをテーマにした問題がよく出題されます。
単価の高い方と安い方のどちらを多く買う予定だったの?
先ほどのリンゴ・ミカンとりちがえ事件を問題にすると、次の通りです。
【例題】太郎君は、1個100円のリンゴと1個40円のミカンを何個か買って、代金は860円になる予定でした。しかし、買う個数をまちがえて逆にしてしまったので、代金は680円になりました。リンゴを何個買いましたか。
例題でまず注意してほしいのは、「リンゴとミカンのどちらを多く買う予定だったのか?」ということです。これは、予定の代金と実際の代金を比べます。
予定の代金より実際の代金が安い場合、単価の高い方を多く買う予定だったとわかります。例題では、860円の予定が実際には680円になっているので、リンゴをミカンより多く買う予定でした。
一方、予定の代金より実際の代金が高い場合、単価の安い方を多く買う予定だったとわかります。

どっちを多く買う予定だったのか、いつも迷ってしまうんですが……。

迷う場合は、簡単な数で考えてみるといい。たとえば、リンゴ1個とミカン2個を買う予定ならば、予定の代金は180円になる。実際にリンゴ2個とミカン1個を買ったとすると、実際の代金は240円だ。単価の安いミカンを単価の高いリンゴより多く買う予定だった場合、予定の代金より実際の代金が高くなっているよね?
表・面積図・消去算のどの解き方がわかりやすいかな?
実際に例題を解いてみましょう。
いくつか解き方を紹介しますので、わかりやすい解き方をマスターしてください!
表を使った解き方
多くの問題集で紹介されている解き方です。
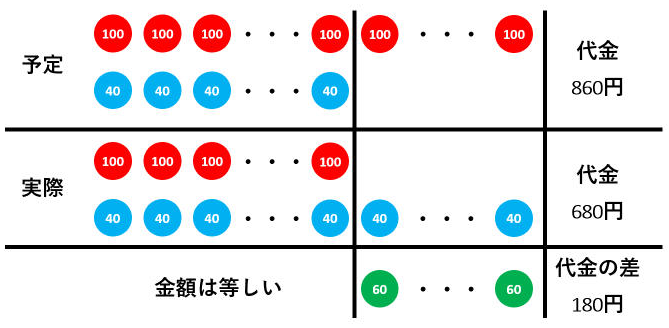
途中まで金額が等しいことに気づけるかどうかがポイントです。
多く買う予定だったリンゴの単価と、実際に多く買ってしまったミカンの単価の差である60円(100円-40円)を集めると、代金の差である180円になります。したがって、実際に多く買ってしまったミカンの個数(=多く買う予定だったリンゴの個数)は、180÷60=3(個)です。
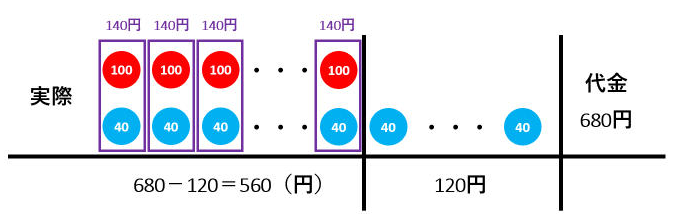
実際の代金からミカン3個分の金額を引くと、680-40×3=560(円)です。また、リンゴ1個とミカン1個をセットにした金額は140円です。この140円が何セットあるかを考えると、560÷140=4(セット)とわかります。
したがって、実際に買ったリンゴの個数は4個です。
面積図を使った解き方
面積図を使って解く場合、リンゴとミカンの単価を縦に、それぞれの個数を横にした長方形を描きます。
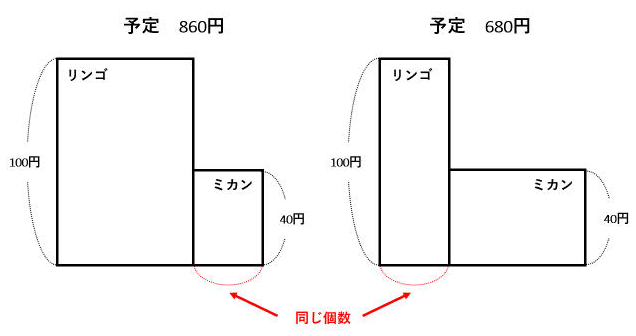
2つの面積図を重ねると、下の図の青い長方形の面積が、代金の差の180円になります。
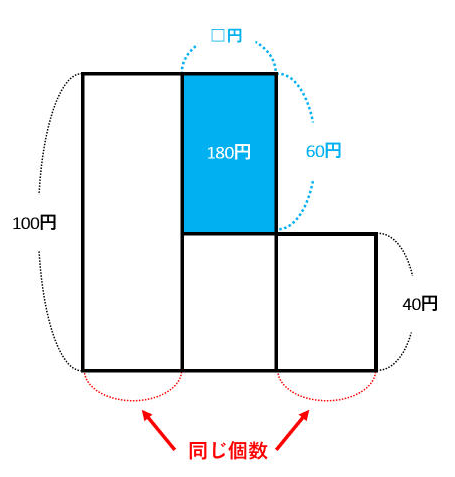
実際に多く買ってしまったミカンの個数(=多く買う予定だったリンゴの個数)は、□=180÷60=3(個)です。
あとは、表を使った解き方と同じなので、560÷140=4より、実際に買ったリンゴの個数は4個です。
消去算を使った解き方
計算力に自信のある受験生は、消去算にもチャレンジしてみましょう。

実際に買ったリンゴを□個、ミカンを△個とする。
予定 100×△+40×□=860 … ①
実際 100×□+40×△=680 … ②
①×2 200×△+80×□=1720 … ③
②×5 200×△+500×□=3400 … ④
④-③より、420×□=1680
したがって、□=1680÷420=4(個)
消去算を使えば、計算だけで答を求められます。表や面積図を使った解き方が苦手な受験生は、消去算を使いこなせるようにするといいでしょう。
代金の差に注目して解く?それとも計算で解く?
とりちがえ問題は、表や面積図から、代金の差がどの部分に対応するかを考えることが大切です。表などから情報を読み取れるようになれば、もっと複雑な差集め算にも対応できるはずです。
一方、「表や面積図を描けない!」「表を描いてもわからない!」という受験生は、計算だけで答を出せる消去算を利用しましょう。消去算は、とりちがえ問題だけでなく、さまざまな問題に応用できる便利な考え方です。力ずくで問題を解く場合にとても役立ちます。
次の質問に答えましょう。(解答例は最後のページにあります)
・とりちがえ問題では、予定の代金と実際の代金を比べると、どのようなことがわかりますか。




コメント