都立高校入試数学平成29年度は、大問5の[問2]の正答率が2.6%でした。本記事では、ほとんどの受験生が解けなかった[問2]を含む大問5を解説します。
線分の長さを求める問題
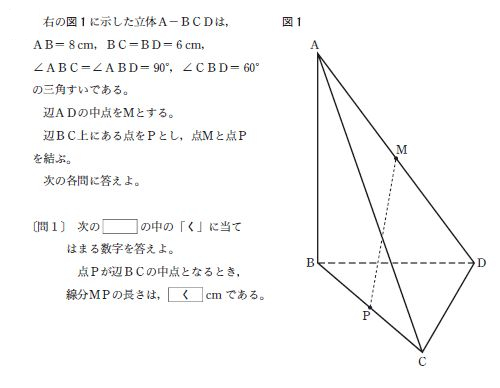
[問1]は、空間図形の中にある線分の長さを求める問題です。このタイプの問題では、「答を求めるためには、どこの線分の長さが必要か?」と考え、必要に応じて補助線を引きます。
また、高校入試レベルの数学では、図形問題の解法として使える武器は、相似を中心とする比、もしくは三平方の定理の2種類しかありません。
[問1]では比を使えそうにありませんので、三平方の定理を使うことにします。MPを一辺とする直角三角形を作るため、MからBDに垂線(補助線)を下ろして、垂線の足をHとします。HとPを結ぶ(補助線)と直角三角形MPHになります。
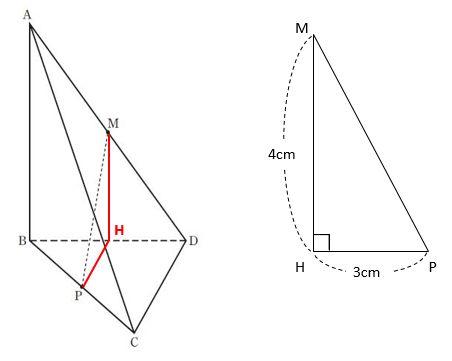
上図の右の三角形は△MPHを抜き書きしたものです。
MとHがそれぞれADとBDの中点なので、中点連結定理よりMH=AB÷2=8÷2=4cmです。
また、△BCDは、BC=BD=6cmで∠CBD=60°なので正三角形です。そのため、CD=6cmと分かります。PとHがそれぞれBCとBDの中点なので、中点連結定理よりPH=CD÷2=6÷2=3cmです。
△MPHに三平方の定理を用いて、MP2=MH2+PH2=42+32=25よりMP=5cmです。
例年、大問5の[問1]は平易な問題が出題されます。しかし、平成29年度は、補助線を引かなければならないため、やや複雑でした。正答率が33.8%だったのは、補助線を引けない受験生が多かったからでしょう。
錐体の体積を求める問題
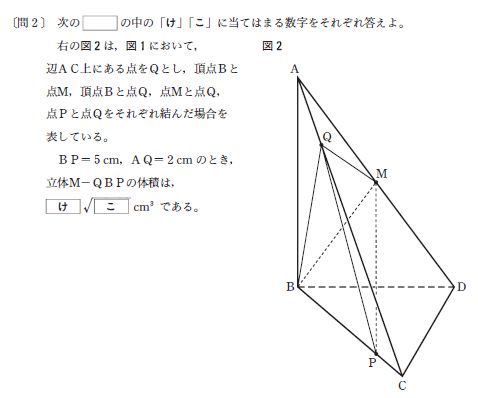
[問2]は、錐体の体積を求める問題です。まずは、錐体の体積の公式を思い出しましょう。
この公式を適用するためには、底面積と高さの値が必要です。問題では立体M‐QBPとあるので、素直に底面を△QBPにしてみます。Mから△QBPに垂直に下した垂線が高さです。
ここで注目すべきは、∠ABC=∠ABD=90°という条件です。これは、立体A‐BCDの面BCDが面ABCに垂直であることを意味します。そして、面BCDに平行な直線は全て面ABCに垂直です。
そこで、下図のように補助線を引いて、面BCDに平行な面MNOと、MからONに下ろした垂線の足Rを作図します。このMRが立体M‐QBPの高さです。
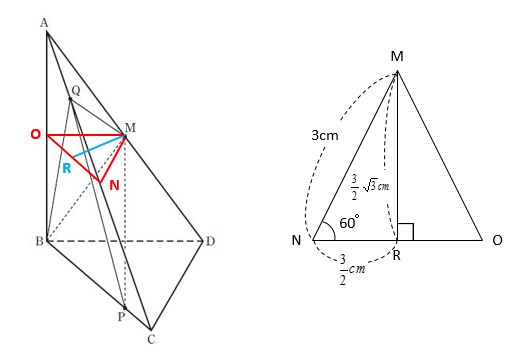
面BCDと面MNOは平行なので面BCD∽面MNOです。そして、中点連結定理より、MN、NO、OMは、それぞれDC、CB、BDの\(\frac{1}{2}\)倍の3cmです。また、面MNOは正三角形なので、特殊な直角三角形の辺の比を用いてMRの長さも求められます(上図右)。
高さを求めたところで、改めて底面である△QBPの面積を求めます。下図のように△QBPを含む△ABCを抜き書きします。
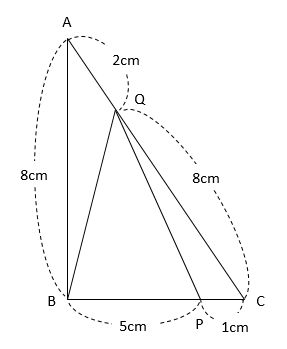
△QBPは△ABCの一部なので、「底辺比=面積比」の関係を利用して、△QBPの面積を求めます。
△ABCは∠B=90°の直角三角形なので、三平方の定理を用いて、AC2=AB2+BC2=82+62=100よりAC=10cmです。したがって、△QBCの面積は、QCを底辺として比を考えると、△ABCの面積の\(\frac{8}{10}\)倍すなわち\(\frac{4}{5}\)倍です。
また、△QBPの面積は、BPを底辺として比を考えると、△QBCの面積の\(\frac{5}{6}\)倍です。
△ABC=8×6÷2=24cm2なので、△QBPの面積は次の通りです。
底面である△QBPの面積と高さであるMRの長さを、錐体の体積を求める公式に当てはめて計算します。
[問2]は、立体を2つに分けたり線分を延長したりする必要のない比較的素直な問題でした。それでも正答率が低かったのは、都教委が分析する通り、「立体の中にできる錐体の底面や高さを正しく捉えることができなかったため」なのでしょう。また、この問題を解くだけの時間的余裕のない受験生が多かったのかもしれません。
空間図形は平面図形に帰着させる
中学数学の中でも、空間図形に関する問題は難易度が高めです。空間の中の線分や面などの位置関係を正しく把握するのが難しいからです。そのため、都教委の指摘する通り、「空間図形を平面図形に帰着させて考える」ことが大切です。
本記事では、空間の中の図形を抜き書きして、平面図形として描き直しました。このように抜き書きすることで空間図形が解きやすくなります。
過去10年の都立高校入試問題を徹底分析して分野別にまとめた問題集「高校入試 虎の巻![]() 」を使って過去問演習を行い、抜き書きのスキルを鍛えましょう。
」を使って過去問演習を行い、抜き書きのスキルを鍛えましょう。
トップ画像=Pixabay




コメント
難しいです
難しいと思うのでしたら、入試本番では大問5[2]に手を出さない方が賢明です。
ほとんどの受験生が解けない問題は捨ててください。