速さの和や差を使って考える「旅人算」には、「出会い」「追い越し」という言葉がよく登場します。そして、これらの言葉のせいで多くの中学受験生が混乱してしまいます。
今回は、旅人算の代表的な2パターンである「出会い算」と「追い越し算」について、もう一度じっくり考えてみましょう。
「出会い算」では速さの和を使うのか？
【例題】A地点とB地点があります。太郎君は分速80m、次郎君は分速60mで同時にA地点を出発しました。次郎君はB地点に向かう途中で、先にB地点を折り返してきた太郎君に出会いました。このとき、次の問いに答えなさい。
(1) AB間の道のりが1400mのとき、2人が出会ったのは出発してから何分後ですか。
(2) B地点の150m手前で2人が出会ったとすると、2人が出会ったのは出発してから何分後ですか。
(1)も(2)も、「次郎君はB地点に向かう途中で、先にB地点を折り返してきた太郎君に出会いました。」という点では同じです。しかし、「どちらも出会い算だから、速さの和を使おう！」と考えるとまちがってしまいます。
まちがうのは、次のような思い込みがあるせいです。
多くの受験生は、「出会う」という言葉を見た瞬間、「速さの和を使う」と考えてしまいます。しかし、実際は、(1)が速さの和を使う問題で、(2)が速さの差を使う問題です。
速さの和を使う問題と速さの差を使う問題では、何が違うのでしょうか？
速さの和を使うのはどういうとき？
速さの和を使う問題と差を使う問題を区別するために、道のりに注目する必要があります。
(1)と(2)のそれぞれについて、状況図（線分図）を描いて、2人の進んだ道のりを見てみましょう。
(1)では、A地点とB地点を線分の両端として、太郎君と次郎君の進んだ道のりを状況図で表しました。
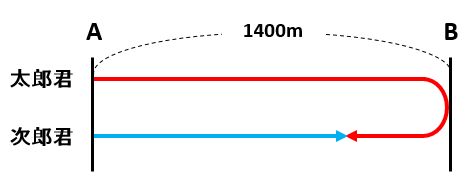
赤い矢印が太郎君の移動した道のり、青い矢印が次郎君の進んだ道のりです。
まずは、2人が出会ったのは□分後として、それぞれの矢印の長さを□で表します。「道のり＝速さ×時間」なので、赤い矢印の長さは80×□、青い矢印の長さは60×□です。
次に、1400mを使うために、赤い矢印の長さと青い矢印の長さを足します。2本の矢印の長さの和が1400mの2倍になっていることに注意しましょう。
80×□＋60×□＝1400×2
分配法則より
（80＋60）×□＝2800
□＝2800÷（80＋60）＝20（分後）
（80＋60）は太郎君と次郎君の速さの和です。したがって、道のりの和を利用する問題では速さの和を使うということがわかります。
速さの差を使うのはどういうとき？
(2)でも、(1)と同じように状況図を描きました。
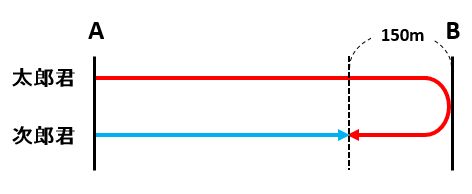
2人が出会ったのは□分後として、赤い矢印の長さは80×□、青い矢印の長さは60×□です。
150mを使うために、赤い矢印の長さから青い矢印の長さを引きます。ここが、(1)とは違うところです。また、2本の矢印の長さの差が150mの2倍になっています。
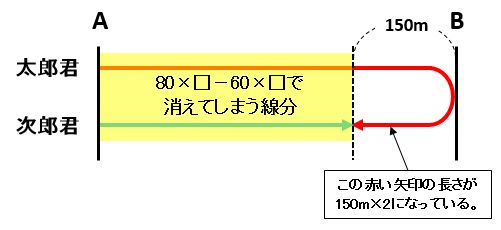
80×□－60×□＝150×2
分配法則より、
（80－60）×□＝300
□＝300÷（80－60）＝15（分後）
（80－60）は、太郎君と次郎君の速さの差です。したがって、道のりの差を利用する問題では速さの差を使うということがわかります。
旅人算では道のりの和や差に注目しよう
旅人算では、道のりの和を考えるときに速さの和を使います。一方、道のりの差を考えるときに速さの差を使います。「出会い」か「追い越し」かは関係ありません。
しかし、多くの算数の問題集や参考書には、「2人が出会う場合は速さの和を使う出会い算で、1人がもう1人を追い越す場合は速さの差を使う追い越し算です」としか書かれていません。そのため、受験生は「出会い」「追い越し」という言葉に引きずられてしまいます。
旅人算で「速さの和を使うの？差を使うの？」と悩んでしまう受験生は、「出会い」「追い越し」という言葉を無視しましょう。そして、状況図を描くなどして、道のりの和と差のどちらを考えればいいのかに注目しましょう。そうすれば、速さの和と差のどちらを使うのかがわかるはずです。
トップ画像＝写真AC
コメント