力の大きさとばねの伸びの関係？フックの法則を使った計算問題の解法

中学受験理科や中学理科の物理分野では「ばね」が頻出です。グラフや表、図が与えられて、それらをもとに計算する問題が出題されます。

ばねの問題は、複数のばねが連結されたり、てこや滑車と組み合わされたりすると複雑になります。しかし、そうでなければ、比例計算を利用した単純な問題になります。

こうした基本問題でも頭を抱える生徒がいます。彼らは、何が原因で詰まってしまうのでしょうか？

ばねののびとばねの長さを理解する

ばねの計算問題を苦手とする生徒たちは、比例計算以前のところで混乱します。次のAとBの問題を区別できないからです。

A. 100gのおもりをつるすと、ばねののびは何cmか。

B. 100gのおもりをつるすと、ばねの長さは何cmか。

Aで問われているのは「ばねののび」で、Bで問われているのは「ばねの長さ」です。

まずは、「ばねののび」と「ばねの長さ」を区別しましょう。

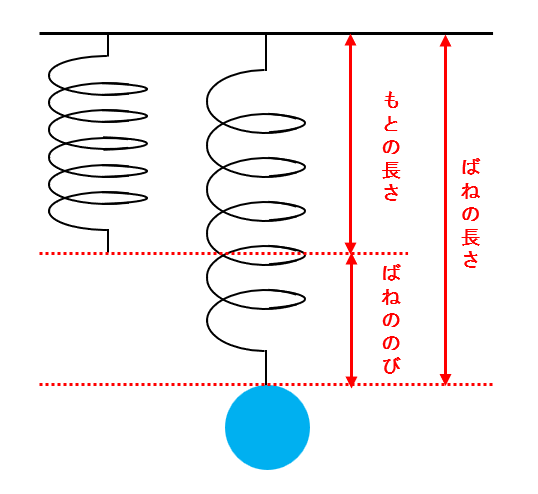
「もとの長さ」は、おもりをつるしていないときのばねの長さです。これは「自然長」と呼ばれることもあります。

「ばねののび」は、おもりをつるしたとき、ばねがもとの長さからどのくらい長くなったか、です。ばねののびには「フックの法則」が成り立ちます。フックの法則とは、ばねにかかる力の大きさ（おもりの重さ）とばねののびは比例する、という法則です。

「ばねの長さ」は、もとの長さとばねののびの和です。ばねの長さではフックの法則が成り立ちません。したがって、ばねの長さは比例計算で求められません。

次に、ばねののびとばねの長さのグラフを考えましょう。

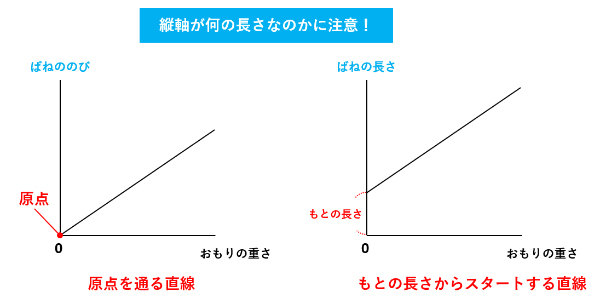
縦軸をばねののび、横軸をおもりの重さとすると、ばねののびとおもりの重さは比例関係なので、原点（（0,0）の点）を通る直線になります。

一方、縦軸をばねの長さ、横軸をおもりの重さとすると、ばねの長さとおもりの重さは比例関係ではないので、（0,もとの長さ）からスタートする直線になります。直線が原点を通らないことに注意しましょう。

最後に、用語の意味が分かれば、次の関係式が成り立つことも分かるはずです。

これらの関係式を丸暗記するのではなく、図と一緒に用語を正確に理解することが大切です。

用語の区別ができたところで、実際にばねの問題を解いてみましょう。

【問題】おもりをつるさないときのもとの長さが違うばねAとばねBがあります。それぞれのばねにおもりをつるしたとき、おもりの重さとばねののびの関係は下のグラフのようになりました。

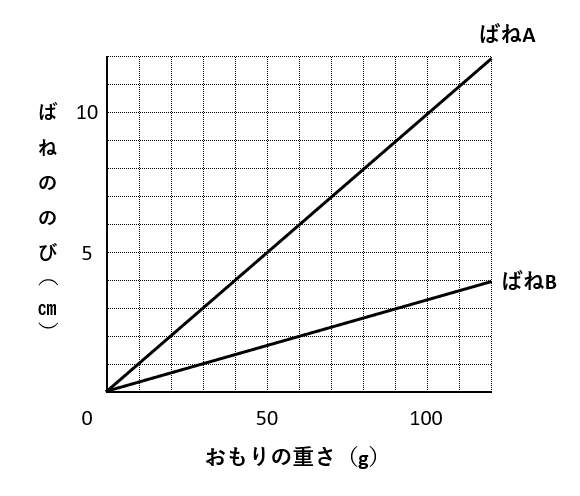
(1) ばねAに80gのおもりをつるすと、ばねの長さは11cmになりました。ばねAのもとの長さは何cmですか。

(2) ばねAとばねBのそれぞれに30gのおもりをつるすと、ばねの長さが同じになりました。ばねBのもとの長さは何cmですか。

(3) ばねBに150gのおもりをつるすと、ばねBの長さは何cmになりますか。

(4) ばねAを(3)と同じ長さにするとき、ばねAにつるすおもりの重さは何gですか。

(1) グラフから、ばねAに80gのおもりをつるすと、ばねAののびは8cmになることが分かります。このとき、ばねAの長さが11cmなので、「もとの長さ＝ばねの長さ－ばねののび」より、ばねAのもとの長さは11－8＝3（cm）です。

(2) ばねAに30gのおもりをつるすと、グラフからばねAののびは3cmです。このとき、「ばねの長さ＝もとの長さ＋ばねののび」より、ばねAの長さは3＋3＝6（cm）です。したがって、30gのおもりをつるしたばねBの長さも6cmです。

ばねBに30gのおもりをつるすと、グラフからばねBののびは1cmです。「もとの長さ＝ばねの長さ－ばねののび」より、ばねBのもとの長さは6－1＝5（cm）です。

ばねののびはおもりの重さに比例することを利用して、ばねBののびを求めます。

グラフから、ばねBに30gのおもりをつるすと、ばねBののびは1cmです。150gは30gの5倍なので、ばねBののびも5倍すると1×5＝5（cm）です。したがって、ばねBに150gのおもりをつるすと、ばねBののびは5cmです。

「ばねの長さ＝もとの長さ＋ばねののび」より、ばねBの長さは5＋5＝10（cm）です。

ばねAを10cmにするには、「ばねののび＝ばねの長さ－もとの長さ」より、ばねAののびを10－3＝7（cm）にする必要があります。

グラフから、ばねAを1cmのばすには、ばねAにつるすおもりの重さは10gです。ばねののびはおもりの重さに比例するので、ばねAを7cmのばすには、ばねAにつるすおもりの重さは10×7＝70（g）です。

トップ画像＝写真AC