問題演習コーナー
【問題】一定の速さで流れる川の上流にあるP地点とその8.4km下流にあるQ地点の間を、静水時の速さがそれぞれ一定である船A、Bが移動します。船AがP地点、船BがQ地点を同時に出発しました。また、出発してから数分後に、船Aから川に浮き輪を落としました。2せきの船は出発してから30分後にすれちがい、それから28分後に船Bは浮き輪とすれちがいました。さらに、その47分後に船BはP地点に着きました。船Aの静水時の速さを毎分160mとして、次の問いに答えなさい。
(1) 川の流れの速さは毎分何mですか。
(2) 船Aから川に浮き輪を落としたのは、船AがP地点を出発してから何分後ですか。
このくらい文章が長いときこそ、ダイヤグラムを描きながら情報を整理することで、「何をすべきか?」が見えてきます。
(1)の解き方(川の流れの速さを求める)
ダイヤグラムを描きましょう。
「上流にあるP地点」「下流にあるQ地点」と書いてあるので、浮き輪が流れる向きはP→Qです。
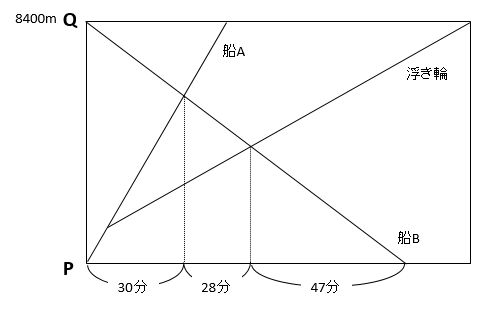
このダイヤグラムから読み取れることをどんどん書き込んでいきます。
まずは、下の図の赤い三角形から、船Aの下りの速さと船Bの上りの速さの比を求めます。道のりが一定なので、時間と速さは逆比です。
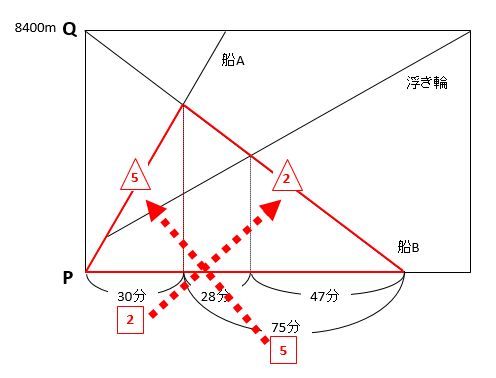
次に、船Bの上りの速さを求めます。船Bが8400mの道のりを105分で移動したことから、船Bの上りの速さは8400m÷105分=分速80mです。
速さと比の関係と使って、船Aの下りの速さも求められます。
船Aの下りの速さ:船Bの上りの速さ=分速□m:分速80m=5:2なので、□=80×5÷2=200です。したがって、船Aの下りの速さは分速200mとわかりました。
「船Aの下りの速さ=船Aの静水時の速さ+川の流れの速さ」です。船Aの静水時の速さを毎分160mなので、川の流れの速さは分速200m-分速160m=分速40mです。

(2)の解き方(浮き輪を落とした時刻を求める)
(2)を解く上で理解しておかなければならないのは、「川の流れの速さ=浮き輪の速さ」です。浮き輪は自分では泳いだりしないので要注意です。
(2)は、ダイヤグラムの中の三角形に注目して、旅人算として考えます。
まずは、下の図の赤い三角形に注目して□mを求めます。
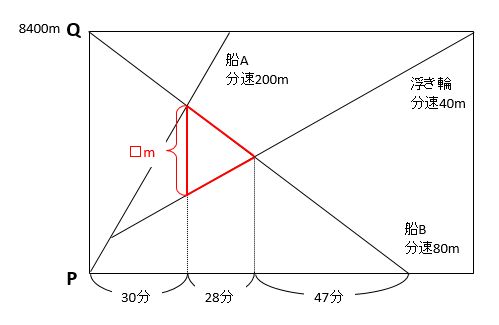
船Bと浮き輪が28分間で進んだときの道のりの和が□mなので、速さの和を使って□m=(分速80m+分速40m)×28分=3360mです。
次に、下の図の青い三角形に注目して△分を求めます。
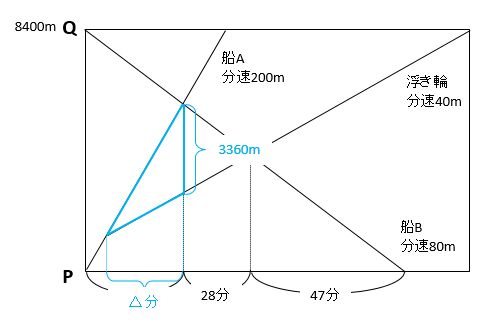
船Aと浮き輪が△分間で進んだときの道のりの差が3360mなので、速さの差を使って、△分=3360m÷(分速200m-分速40m)=21分です。
以上より、30分-21分=9分後が答です。
トップ画像=Pixabay



コメント