【過不足算】長椅子問題も簡単に解ける！席数の余りと不足に注目せよ

過不足算の応用に「長いす問題」があります。多くの中学受験生が苦手とする長いす問題の解き方を紹介します。

過不足算が苦手な場合は、先に以下の記事で基本を確認しましょう。

【過不足算】線分図や面積図を描けば個数や人数を簡単に求められる！

あまりや不足をヒントに人数や個数を求める過不足算では、「あまりや不足を足すの？引くの？」と混乱しないように、線分図や面積図を描きましょう。

mimizuku-edu.com

2016.01.27

オカルト進学塾

志望校合格とオカルトエリートを目指す受験勉強サイト

occult-shingakujuku.com

人数ではなく席数に注目しよう

過不足算では、1人あたりの個数の差と全体の個数の差を比べて人数を求める解き方が有名です。

しかし、【例題】では、子ども1人あたりの個数の差などを考えようとすると、わけがわからなくなります。そこで、子どもではなくいすに注目して、いす1脚あたりの席数の差と全体の席数の差を考えます。

1脚あたりの席数の差は7ー5＝2席です。

「1脚に7人ずつ座ると、3人がけのいすが1脚できて、さらに1脚あまります」から、あまる席数を求めます。「3人がけのいすが1脚できて」から、7ー3＝4席あまります。さらに1脚分の7席もあまっているので、あまる席数は合計で4＋7＝11席です。

一方、「1脚に5人ずつ座ると15人が座れません」から、不足する席数は15席です。

全体の席数の差は、あまりと不足の和で11＋15＝26席です。

「いすの数＝全体の席数の差÷いす1脚あたりの席数の差」より、いすは26÷2＝13脚です。また、子どもの人数は5×13＋15＝80人です。

線分図を描いて解いてみよう

2本の線を子どもの人数（子ども全員が座れる席数）、いすの数を□脚とします。

上の線には、7人ずつ□脚に座ったときの席数（7×□席）とあまる席数（11席）を書き込みました。

同じように、下の線には5人ずつ□脚に座ったときの席数（5×□席）と不足する席数（15席）を書き込みました。

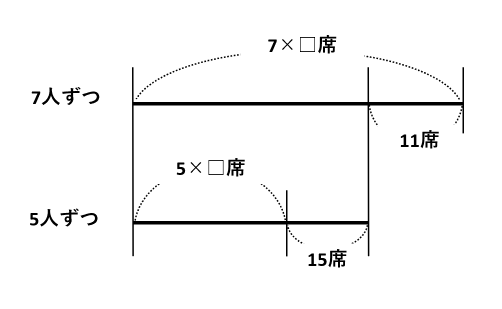
線分図を見ながら、7×□ー5×□＝（7ー5）×□＝2×□席と11＋15＝26席を書き足しましょう。

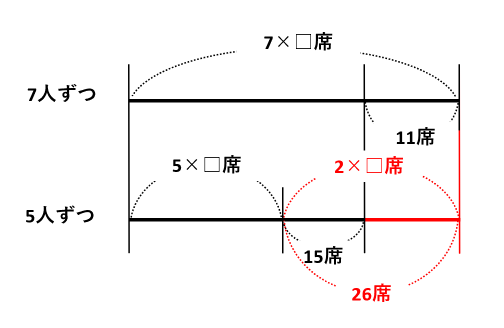
2×□＝26なので、□＝26÷2＝13脚がいすの数です。また、子どもの人数は5×13＋15＝80人です。

面積図を描いて解いてみよう

縦に1脚あたりの席数、横にいすの数を書いた面積図を描きます。

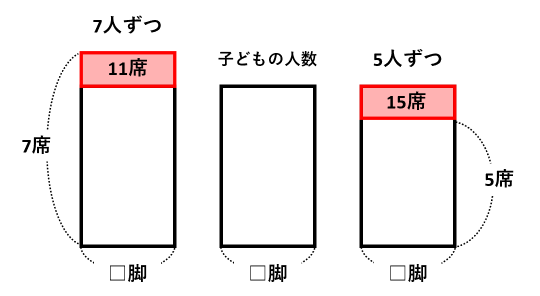
これら3つの図を1つに合わせると、次の図になります。

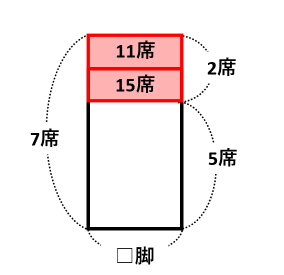
11＋15＝26席の長方形を見て、2×□＝26から□＝26÷2＝13脚がいすの数です。また、子どもの人数は5×13＋15＝80人です。