問題演習コーナー
【例題】下の図は一辺の長さが1cmの正方形をつなげて作った図形です。この図形を直線ℓを回転の軸として1回転させてできる立体の体積と表面積を求めなさい。ただし、円周率は3.14とします。
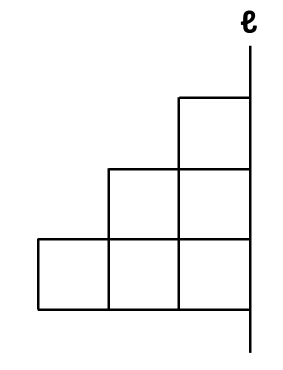

回転体の見取り図を描くと下のようになります。
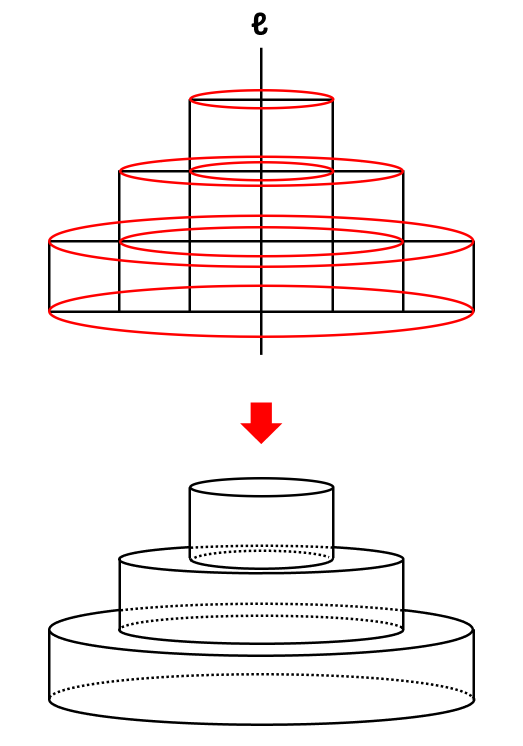
回転体の体積を求めよう
まずは、体積から求めます。
回転体は、高さが1cmの円柱が3つ重なっています。3つの円柱について、底面の円の半径はそれぞれ1cm、2cm、3cmです。
したがって、回転体の体積は、1×1×3.14×1+2×2×3.14×1+3×3×3.14×1=(1+4+9)×3.14=14×3.14=43.96cm3です。
回転体の表面積を求めよう
次に、表面積を求めます。
回転体を真上から見た図と真下から見た図、3つの円柱の側面積は下のようになります。
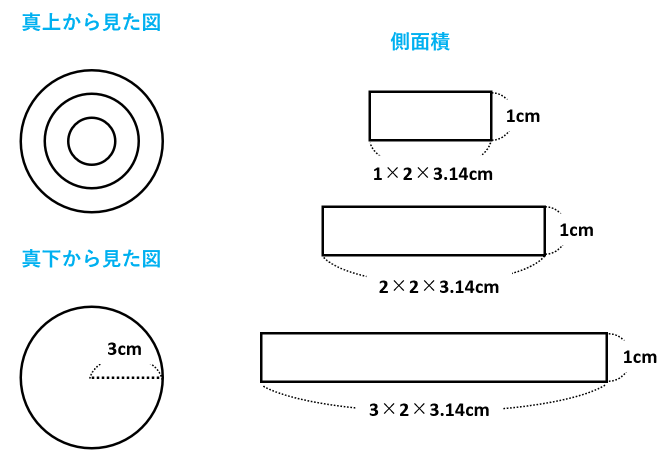
真上から見た図は、3つの円が重なっています。しかし、表面積に含まれる部分の面積だけを考えると、真下から見た図の面積と同じです。つまり、半径3cmの円の面積が2つ、表面積に含まれます。
したがって、回転体の表面積は、(半径3cmの円の面積)×2+(側面積の和)=3×3×3.14×2+1×2×3.14×1+2×2×3.14×1+3×2×3.14×1=(18+2+4+6)×3.14=30×3.14=94.2cm2です。
トップ画像=Pixabay



コメント