中学数学の平面図形分野では、平行移動や対称移動などの作図があります。中学1年生にとって、特に回転移動が難しいようです。
回転移動とは、ある点を中心に図形を一定の角度だけ移動させることです。
白紙上で図形を回転させる場合、コンパスや分度器を使います。しかし、マス目のある用紙を利用した回転移動の作図では、基本的に定規だけを使用します。その作図方法を解説します。
マス目を利用して回転移動を作図
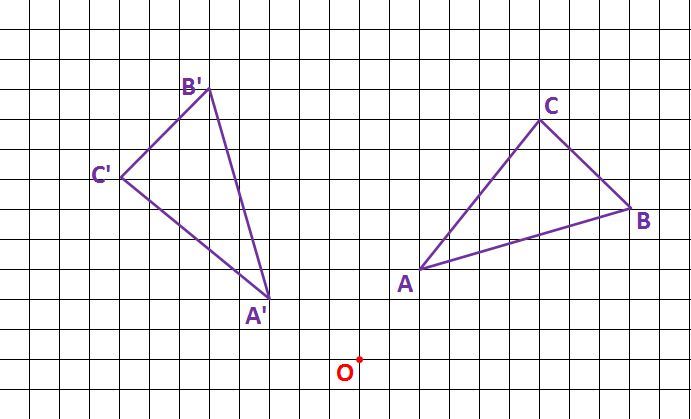
下図の三角形ABCを点Oを中心に反時計回りに90°回転させてできる三角形A’B’C’を作図しなさい。
マス目を利用して図形を回転させる場合、回転の中心Oと三角形の頂点を結んで考えると分かりやすいですよ。
まずは、Oと頂点Aを結んでみます。
OAを反時計回りに90°回転させた先が、三角形A’B’C’の頂点A’となります。OA=OA’の関係が成り立ちます。
このことを意識しながら、実際にOAを反時計回りに90°回転させると……
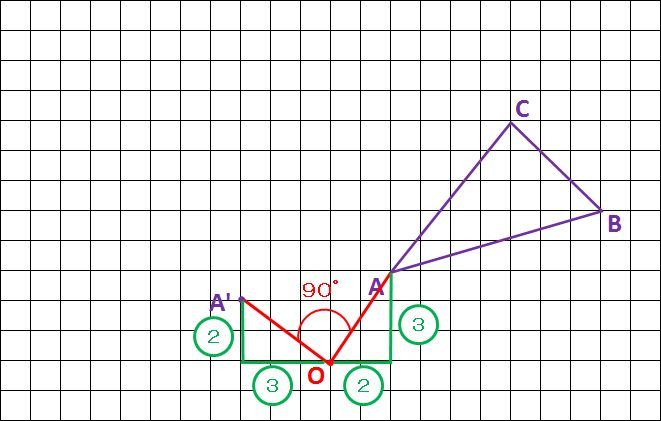
OAと等しい長さのOA’を描くときにマス目を利用します。OからAまでの長さを測る場合、「Oから右に2マス、上に3マス」と考えます。定規でOAの長さを測らないでくださいね。
マス目の数をもとにA’の位置を確定します。「Oから左に3マス、右に2マス」の位置がA’です。
90°回転の場合、もとの頂点と移動先の頂点に関して、Oと頂点との距離は、横方向と縦方向のマス目の数が入れ替わります。
このことが分かれば、B’とC’も作図できます。
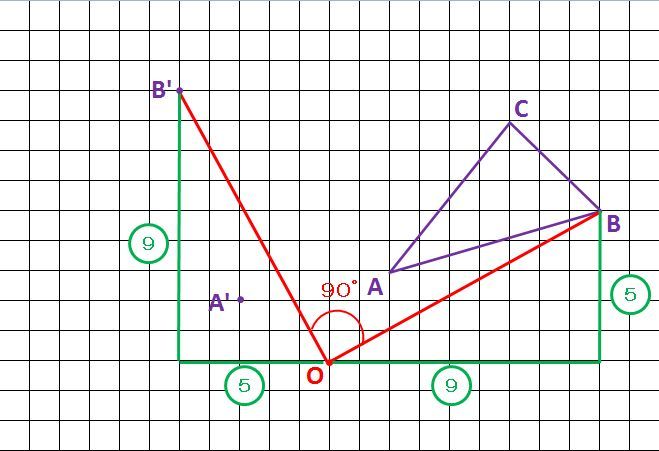
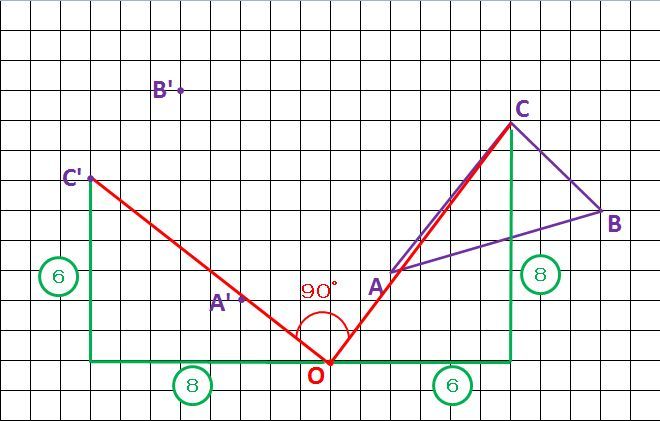
3点A’,B’,C’を結ぶと三角形A’B’C’の完成!!
以上のような作図問題は定期試験でもときどき出題されます。中学1年生は、回転移動の作図方法をしっかりマスターしてくださいね。
トップ画像=Pixabay




コメント