何個かのものを何人かにわけるとき、ものがあまったり不足したりすることがあります。このあまりや不足の個数をヒントに人数やもの全体の個数を求める問題が「過不足算」です。
過不足算では、ものがあまったり、不足したり、ちょうど全員に行きわたったりします。そのため、多くの中学受験生が「あまりや不足を足すの?引くの?」と混乱します。
そんな受験生のために、過不足算のさまざまな解き方を解説します。
個数の差を利用して解いてみよう
過不足算では、1人あたりの個数の差と全体の個数の差を比べて人数を求める解き方が有名です。
【例題】では、1人あたりの個数の差は9ー5=4個です。一方、あまりが45個と13個なので、全体の個数の差はあまり同士の差で45ー13=32個です。
1人あたりの個数の差が人数分集まって全体の個数の差になっています。したがって、「人数=全体の個数の差÷1人あたりの個数の差」より、32÷4=8人です。また、あめ玉の個数は5×8+45=85個です。
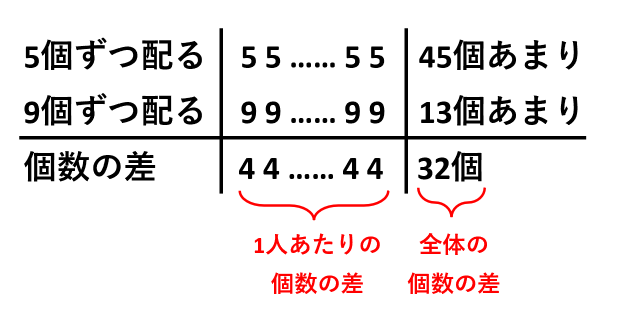
個数の差を利用する解き方は、慣れてしまえば簡単です。ただ、全体の個数の差を求めるとき、足すのか引くのかでわからなくなりがちです。
今回のように「あまり同士の差」などといわれて納得できない受験生は、この後で紹介する線分図や面積図で考えるようにしましょう。
線分図を描いて解いてみよう
過不足算も線分図を描いてみるとわかりやすくなります。
過不足算の線分図は、同じ長さの2本の線を描くことから始まります。この2本の線は全体の個数を表します。【例題】では、全体の個数はあめ玉の個数です。
次に、ものを受け取る人たちの人数を□人とします。【例題】では、あめ玉を受け取る人たちの人数が□人です。
ここまで決めたら、線分図を描いてみましょう。
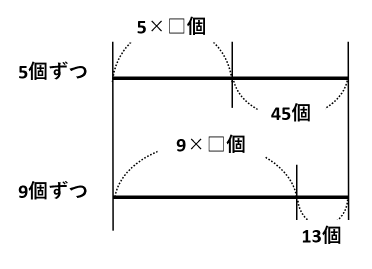
上の線には、5個ずつ□人に配った個数(5×□個)とあまり(45個)を書き込みました。

あまりの45個は、線の右端を切り取るように書くのよ。線を右側に伸ばしちゃダメ!
同じように、下の線には9個ずつ□人に配った個数(9×□個)とあまり(13個)を書き込みました。

□を使った個数は、線の上に書くか、下に書くか、ルールを決めて書こう。□を使った個数を、上の線では下に書いて、下の線分では上に書く、みたいにすると、わかりにくくなるよ。
線分図を見ながら、9×□ー5×□=(9ー5)×□=4×□個と45ー13=32個を書き足しましょう。
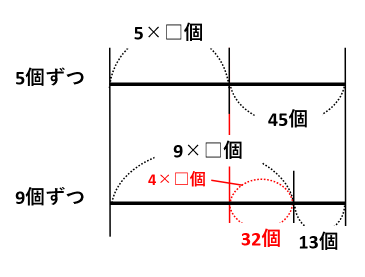
4×□=32なので、□=32÷4=8人が人数です。また、あめ玉の個数は5×8+45=85個です。
線分図を描いてみると、全体の個数の差があまり同士の差になる理由に納得できるはずです。
面積図を描いて解いてみよう
過不足算は面積図でも解けます。
面積図を描くときは、縦に1人あたりの個数、横に人数を書くとよいでしょう。

縦に人数、横に1人あたりの個数を書いちゃダメなんですか?

ダメではないよ。ただ、他の特殊算でも面積図を使うことを考えると、縦に単位量あたりの大きさ(1に対応する数)を書くのがオススメなんだ。

つるかめ算では、縦につる1羽の足の数とかめ1匹の足の数を書きました。1匹(羽)の足の数が単位量あたりの大きさですね!


その通り。他にも速さや平均、単価(1個の値段)などを面積図の縦に書くことが多いよ。
わかりやすいように、あめ玉の個数の面積図を描き、それとは別に5個ずつ配る場合と9個ずつ配る場合を描いてみました。赤い部分がそれぞれあまりの個数です。
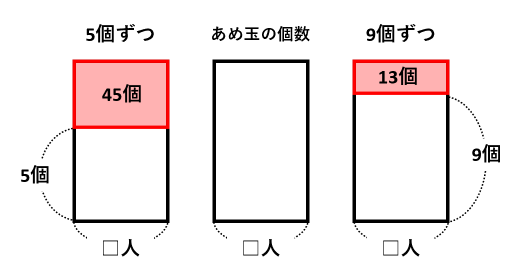
これら3つの図を1つに合わせると、次の図になります。
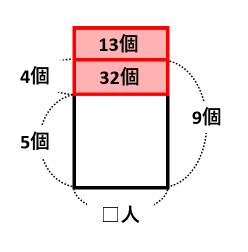
45ー13=32個の長方形を見て、4×□=32から□=32÷4=8人が人数です。また、あめ玉の個数は5×8+45=85個です。
悩むなら図を描いて考えよう
過不足算で「あまりと不足は足す、あまりとあまりは引く、不足と不足は引く」を公式のように覚えている受験生がいます。
覚えること自体は悪くありません。しかし、「どうして足す(引く)のか?」がわからないまま丸暗記するのは好ましくありません。少しひねられただけで混乱するからです。
足したり引いたりするのに悩む受験生には、線分図や面積図を描いて考えることをお勧めします。
次の質問に答えましょう。(解答例は最後のページにあります)
① 過不足算で人数を求めるには何と何を比べますか。
② 過不足算の線分図では何を2本の線で表しますか。
③ 過不足算では何を□としますか。
③ 過不足算の面積図では長方形の縦と横にそれぞれ何を書きますか。




コメント